Distances

Distance between vectors

Euclidean distance: Euclidean distance is a measure of the true straight line distance between two points in Euclidean space. (source )

The Euclidean distance between vectors

and

is defined as:

A common way to calculate the distance between two points in high dimensional space is by using Euclidean distance.

The formula to calculate Euclidean distance is shown.

Given two vectors or two features vectors, in our case, we are assuming we have two feature vectors named 𝑢 and 𝑣.

The Euclidean distance between them is defined by the square root of the summation of the squared element-wise differences between these two factors (A mouthful, we know, we will look at the steps in the next few slides).

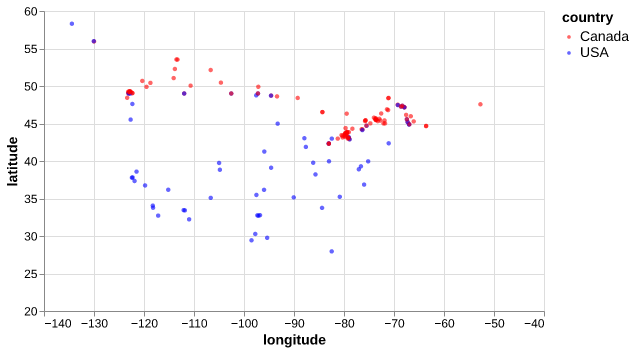
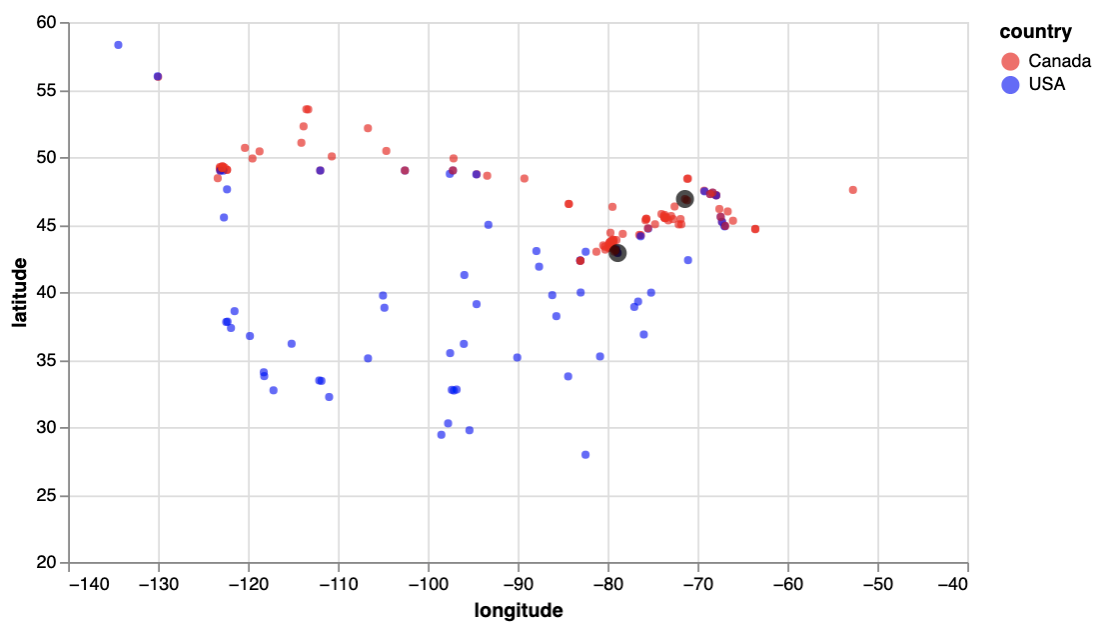
cities_df = pd.read_csv("data/canada_usa_cities.csv")
train_df, test_df = train_test_split(cities_df, test_size=0.2, random_state=123)
train_df.head()

	longitude	latitude	country
160	-76.4813	44.2307	Canada
127	-81.2496	42.9837	Canada
169	-66.0580	45.2788	Canada
188	-73.2533	45.3057	Canada
187	-67.9245	47.1652	Canada

Let’s return to the cities dataset that we have been working with.

As a reminder, the data set has two features: longitude and latitude and we are trying to predict if the city is in the USA or Canada.

cities_viz = alt.Chart(train_df, width=500, height=300).mark_circle(size=20, opacity=0.6).encode(
    alt.X('longitude:Q', scale=alt.Scale(domain=[-140, -40])),
    alt.Y('latitude:Q', scale=alt.Scale(domain=[20, 60])),
    alt.Color('country:N', scale=alt.Scale(domain=['Canada', 'USA'],
                                           range=['red', 'blue']))
)
cities_viz

Here is the plot showing Canadian cities in red and American cities in blue.

two_cities = cities_df.sample(2, random_state=42).drop(columns=["country"])
two_cities

	longitude	latitude
30	-66.9843	44.8607
171	-80.2632	43.1408

Let’s take 2 points (two feature vectors) from the cities dataset.

The two sampled points are shown as black circles.

Our goal is to find how similar these two points are.

How do we calculate the distance between the two cities?

two_cities

	longitude	latitude
30	-66.9843	44.8607
171	-80.2632	43.1408

Subtract the two cities:

two_cities.iloc[1] - two_cities.iloc[0]

longitude   -13.2789
latitude     -1.7199
dtype: float64

Square the differences:

(two_cities.iloc[1] - two_cities.iloc[0])**2

longitude    176.329185
latitude       2.958056
dtype: float64

How do we calculate the distance between these two points (two cities)?

Let’s calculate the Euclidean distance between these two cities so here are our two cities.

The first step is to subtract these two cities. We are subtracting the city at index 0 from the city at index 1.

Next, we square the differences.

Sum them up:

((two_cities.iloc[1] - two_cities.iloc[0])**2).sum()

np.float64(179.28724121999983)

And then take the square root:

np.sqrt(np.sum((two_cities.iloc[1] - two_cities.iloc[0])**2))

np.float64(13.389818565611703)

Our third step is summing up the squared differences.

Then finally we take the square root of the value.

This results in a value of 13.3898 which is the distance between the two cities.

np.sqrt(np.sum((two_cities.iloc[1] - two_cities.iloc[0])**2))

np.float64(13.389818565611703)

from sklearn.metrics.pairwise import euclidean_distances

euclidean_distances(two_cities)

array([[ 0.        , 13.38981857],
       [13.38981857,  0.        ]])

sklearn has a function called euclidean_distances that we could use instead of going through each of the steps on the previous slide.

When we call this function on our two cities data, it outputs this matrix with four values.

• Our first value is the distance between city 0 and itself.
• Our second value is the distance between city 0 and city1.
• Our third value is the distance between city 1and city 0.
• Our fourth value is the distance between city 1 and itself.

As we can see, the distances are symmetric. If we calculate the distance between city 0 and city, it’s going to have the same value as if we calculated the distance between city 1 and city 0.

This isn’t always the case if we use a different metric to calculate distances.

Let’s apply what we learned!