Precision, Recall and F1 Score

Accuracy is only part of the story…

from sklearn.pipeline import make_pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.tree import DecisionTreeClassifier

pipe_tree = make_pipeline(
    (StandardScaler()),
    (DecisionTreeClassifier(random_state=123))
)

from sklearn.model_selection import cross_validate
pd.DataFrame(cross_validate(pipe_tree, X_train, y_train, return_train_score=True)).mean()

fit_time       9.988710
score_time     0.005139
test_score     0.999119
train_score    1.000000
dtype: float64

y_train.value_counts(normalize=True)

Class
0    0.998302
1    0.001698
Name: proportion, dtype: float64

We have been using .score to assess our models, which returns accuracy by default.

Accuracy is misleading when we have a class imbalance.

We need other metrics to assess our models.

We’ll discuss three commonly used metrics which are based on the confusion matrix:

• recall
• precision
• f1 score

Note that these metrics will only help us assess our model.

Later we’ll talk about a few ways to address the class imbalance problem.

from sklearn.metrics import confusion_matrix

pipe_tree.fit(X_train,y_train);
predictions = pipe_tree.predict(X_valid)
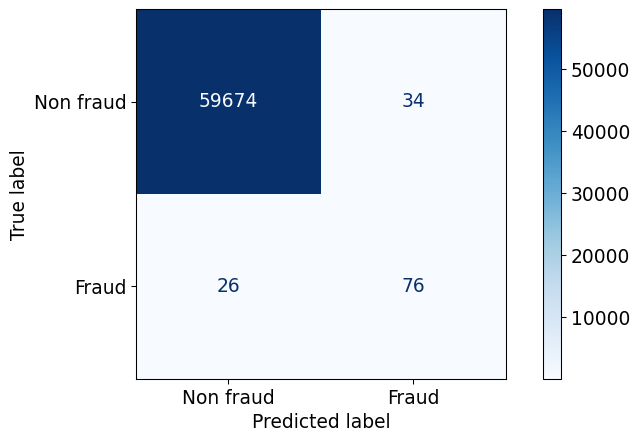
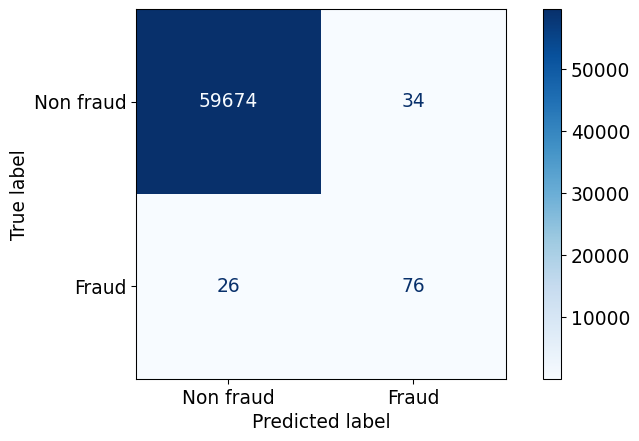
confusion_matrix(y_valid, predictions)

array([[59674,    34],
       [   26,    76]])

TN, FP, FN, TP = confusion_matrix(y_valid, predictions).ravel()

Let’s build our pipeline, and fit it. Once we’ve done that, we can create our confusion matrix.

This time we are going to split up the values in the matrix into the 4 quadrants we saw earlier.

• TN for the True Negatives
• FP for the False Positives
• FN for the False Negatives
• TP for the True Positives

We need each of these values to explain the next measurements.

• The .ravel() function “flattens” or “unravels” the matrix into a 1D array which makes it easier to obtain the individual values.

Recall

Among all positive examples, how many did you identify?

Recall: how many of the actual positive examples did you identify?

So, in this case, since fraud is our positive label, we see the correctly identified labels in the bottom right quadrant and the ones that we missed in the bottom left quadrant.

confusion_matrix(y_valid, predictions)

array([[59674,    34],
       [   26,    76]])

TN, FP, FN, TP = confusion_matrix(y_valid, predictions).ravel()

recall = TP / (TP + FN)
recall.round(4)

np.float64(0.7451)

So here we take our true positives and we divide by all the positive labels in our validation set which is the predictions the model incorrectly labeled as negative (the false negatives).

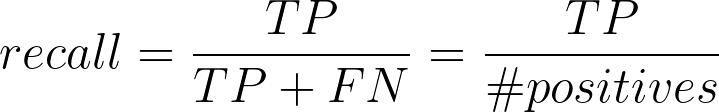
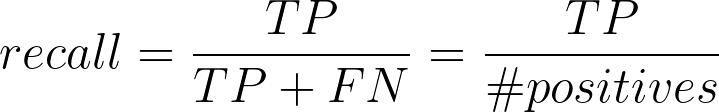
Precision

Among the positive examples you identified, how many were actually positive?

Precision: Of the frauds we “caught”, the fraction that was actually frauds.

With fraud as our positive label, we see the correctly identified fraud in the bottom right quadrant and the labels we incorrectly labeled as frauds in the top right.

confusion_matrix(y_valid, predictions)

array([[59674,    34],
       [   26,    76]])

TN, FP, FN, TP = confusion_matrix(y_valid, predictions).ravel()

precision = TP / (TP + FP)
precision.round(4)

np.float64(0.6909)

So here we take our true positives and we divide by all the positive labels that our model predicted.

Of course, we’d like to have high precision and recall but the balance depends on our domain.

For credit card fraud detection, recall is really important (catching frauds), precision is less important (reducing false positives).

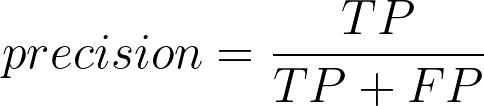
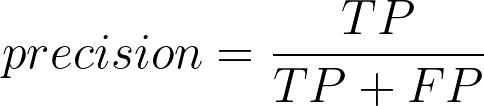
f1

f1-score combines precision and recall to give one score.

f1: The harmonic mean of precision and recall.

f1-score combines precision and recall to give one score. which could be used in hyperparameter optimization, for instance.

precision

np.float64(0.6909090909090909)

recall

np.float64(0.7450980392156863)

f1_score = (2 * precision * recall) / (precision + recall)
f1_score

np.float64(0.7169811320754716)

If both precision and recall go up, the f1 score will go up, so in general, we want this to be high.

Sometimes we need a single score to maximize, e.g., when doing hyperparameter tuning via RandomizedSearchCV.

Accuracy is often a bad choice.

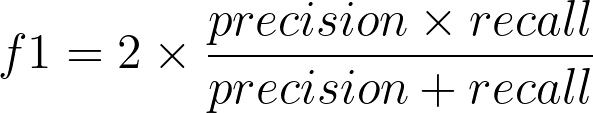
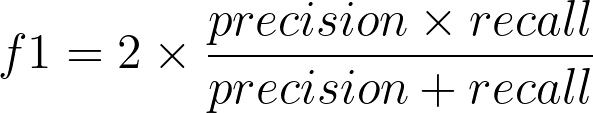
Calculate evaluation metrics by ourselves and with sklearn

data = {}
data["accuracy"] = [(TP + TN) / (TN + FP + FN + TP)]
data["error"] = [(FP + FN) / (TN + FP + FN + TP)]
data["precision"] = [ TP / (TP + FP)] 
data["recall"] = [TP / (TP + FN)] 
data["f1 score"] = [(2 * precision * recall) / (precision + recall)] 
measures_df = pd.DataFrame(data, index=['ourselves'])

We can calculate all these measurements ourselves using basic math, or…

from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score

pred_cv =  pipe_tree.predict(X_valid) 

data["accuracy"].append(accuracy_score(y_valid, pred_cv))
data["error"].append(1 - accuracy_score(y_valid, pred_cv))
data["precision"].append(precision_score(y_valid, pred_cv, zero_division=1))
data["recall"].append(recall_score(y_valid, pred_cv))
data["f1 score"].append(f1_score(y_valid, pred_cv))

pd.DataFrame(data, index=['ourselves', 'sklearn'])

	accuracy	error	precision	recall	f1 score
ourselves	0.998997	0.001003	0.690909	0.745098	0.716981
sklearn	0.998997	0.001003	0.690909	0.745098	0.716981

…We can use scikit-learn which has functions for these metrics.

See here.

The scores match.

Classification report

from sklearn.metrics import classification_report

pipe_tree.classes_

array([0, 1])

print(classification_report(y_valid, pipe_tree.predict(X_valid),
        target_names=["non-fraud", "fraud"]))

              precision    recall  f1-score   support

   non-fraud       1.00      1.00      1.00     59708
       fraud       0.69      0.75      0.72       102

    accuracy                           1.00     59810
   macro avg       0.85      0.87      0.86     59810
weighted avg       1.00      1.00      1.00     59810

There is a convenient function called classification_report in sklearn which gives the information that we described earlier.

We can use classes to see which position each label takes so we can designate them more comprehensive labels in our report.

Note that what you consider “positive” (fraud in our case) is important when calculating precision, recall, and f1-score.

If you flip what is considered positive or negative, we’ll end up with different True Positive, False Positive, True Negatives and False Negatives, and hence different precision, recall, and f1-scores.

The support column just shows the number of examples in each class.

See here for full size.

We’ve provided you with a “Cheat Sheet” that you can refer to.

It will be available here.

Accuracy is misleading when you have a class imbalance.

A confusion matrix provides a way to break down errors made by our model.

We have looked at three metrics based on the confusion matrix:

• precision
• recall
• f1-score

Let’s apply what we learned!