Output, Results and Discussions

Model Selection

In order to predict heart disease in patients based on the different health indicators provided in the dataset, we decided to try two different models, LogisticRegression and SVC (support vector classifier), with default parameters as well as the DummyClassifier as a base model for comparison. We conducted 5-fold cross validation on the train set and extracted the mean fit time, score time, test score and train score for each model as well as the standard deviations to compare the models and select one for hyperparameter optimization. We used the f1 score as opposed to accuracy as our scoring metric due to the class imbalance we observed during our EDA. The results are listed in the table below:

import pandas as pd

pd.read_csv("../../results/model_selection_results.csv", index_col=0)

	dummy	SVM	log_reg
fit_time	0.001 (+/- 0.000)	0.004 (+/- 0.002)	0.003 (+/- 0.000)
score_time	0.001 (+/- 0.000)	0.002 (+/- 0.000)	0.001 (+/- 0.000)
test_score	0.726 (+/- 0.007)	0.870 (+/- 0.038)	0.836 (+/- 0.012)
train_score	0.726 (+/- 0.002)	0.908 (+/- 0.003)	0.885 (+/- 0.008)

Table 1: Cross validation and Train mean f1 scores and standard deviation by model

Based on these results, we could see that the DummyClassifier model already performs quite well at predicting the presence of disease. However, both SVC and LogisticRegession had higher mean cross validation f1 scores and were already performing better than the DummyClassifier with default values. SVC has the higher mean cross validation f1 score compared to LogisticRegression so we decided to continue with this model for downstream hyperparameter tuning.

Hyperparameter Optimization

To conduct hyperparameter optimization, we decided to use RandomizedSearchCV with 50 iterations to search through optimal values for C and gamma for the SVC model. We used the loguniform distribution from \(10^{-3}\) to \(10^3\) for both hyperparameters. We also looked at f1, recall, and precision scores to compare the models. The mean cross validation f1 scores from the top 5 results of this search are listed below:

optim_df = pd.read_csv("../../results/optimization_results.csv", index_col=0)
optim_df = optim_df.iloc[:,0:5].T
optim_df.iloc[:,0:8]

	mean_fit_time	mean_score_time	param_svc__C	param_svc__gamma	mean_test_f1	std_test_f1	mean_train_f1	std_train_f1
1	0.003021	0.002237	5.542653	0.004940	0.870002	0.036278	0.885719	0.008873
2	0.006642	0.002319	2.191347	0.008990	0.864217	0.036591	0.879164	0.005463
3	0.003079	0.002318	0.358907	0.074742	0.857567	0.037695	0.894765	0.004161
4	0.003282	0.002430	0.768407	0.225271	0.857033	0.033634	0.951647	0.006082
5	0.003143	0.002173	113.254281	0.003156	0.854928	0.025702	0.898059	0.006965

Table 2: Cross validation and Train mean f1 scores and standard deviation of top 5 models

After the joint hyperparameter optimization, the C and gamma values that gave the best mean test and train scores were 5.542653 for C and 0.004940 for gamma. We did not get an f1 score higher than the default SVC model, but we can see that there is a range in the difference between the validation scores and train scores even when just looking at the top 5 models. This data can help us ensure our model is neither underfit nor overfit and performs as well as possible without being overly complex. The recall and precision scores of the top 5 models are listed below:

optim_df = optim_df.drop(
    ["rank_test_recall", "rank_test_precision"],
    axis=1,
).rename(columns={"std_test_recall":"std", "std_train_recall":"std", "std_test_precision":"std", "std_train_precision": "std"})
optim_df.iloc[:, 8:]

	mean_test_recall	std	mean_train_recall	std	mean_test_precision	std	mean_train_precision	std
1	0.941799	0.043671	0.954709	0.011475	0.809546	0.043052	0.826077	0.009085
2	0.941799	0.043671	0.949271	0.012293	0.799584	0.043485	0.818798	0.005595
3	0.927513	0.022625	0.954709	0.008097	0.799002	0.057458	0.842102	0.012343
4	0.905820	0.017576	0.980066	0.006777	0.813958	0.048279	0.924971	0.012734
5	0.898148	0.043807	0.942031	0.015798	0.817520	0.032966	0.858261	0.010438

Table 3: Cross validation and Train mean recall and precision scores and standard deviation of top 5 models

We can see that our recall scores are higher than our precision scores with this model. Since our problem is related to disease detection, we are more concerned with keeping recall high as we are care most about reducing false negatives. A false negative in this case will involve predicting no heart disease when heart disease is indeed present which is quite dangerous.

Test Results

After we had a model we were reasonably confident in, we assessed it using our test data. We achieved a f1 score of about 0.81 which is consistent with our cross-validation results and means we can be relatively confident in our model’s performance to predict heart disease on deployment data. Below we have included the confusion matrix based on our test data to help visualize its performance:

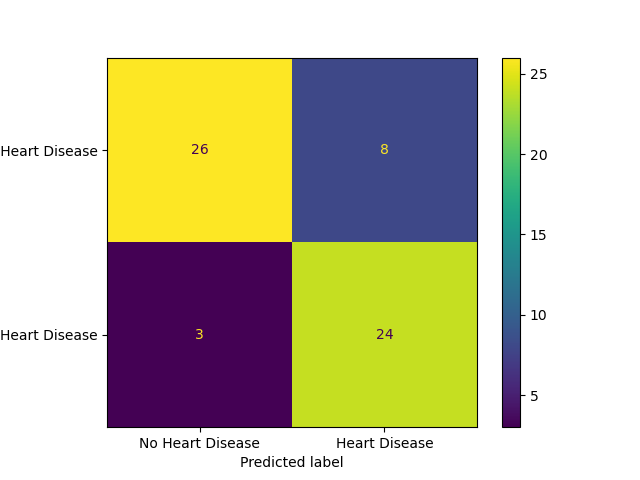
Figure 5: Confusion matrix of model performance on the test set

Conclusions

In conclusion, the SVC model seems to be a good candidate for this heart disease prediction task. The gap between cross-validation scores and test scores was only about 6% so we are hopeful this model will be effective on deployment data as well. However, as our dataset was relatively small, it would be interesting to see how this model would scale up and whether the limited data used in both training and testing would impact the results.

Limitations & Future Work

In future, it would be good to try out a wider variety of models such as RandomForestClassifier or linearSVC and conduct hyperparameter optimization on multiple models before making a decision on which model to select. It would also be interesting to use LogisticRegression to look at feature importances and see if we can simplify our model by removing features with less relevance while still achieving similar results. Having a larger dataset to work with during training may also improve our model and improve its performance in deployment.