PageRank as a Markov model

PageRank as a Markov model#

PageRank: intuition#

Important webpages are linked from other important webpages.
Don’t just look at the number of links coming to a webpage but consider who the links are coming from

Credit

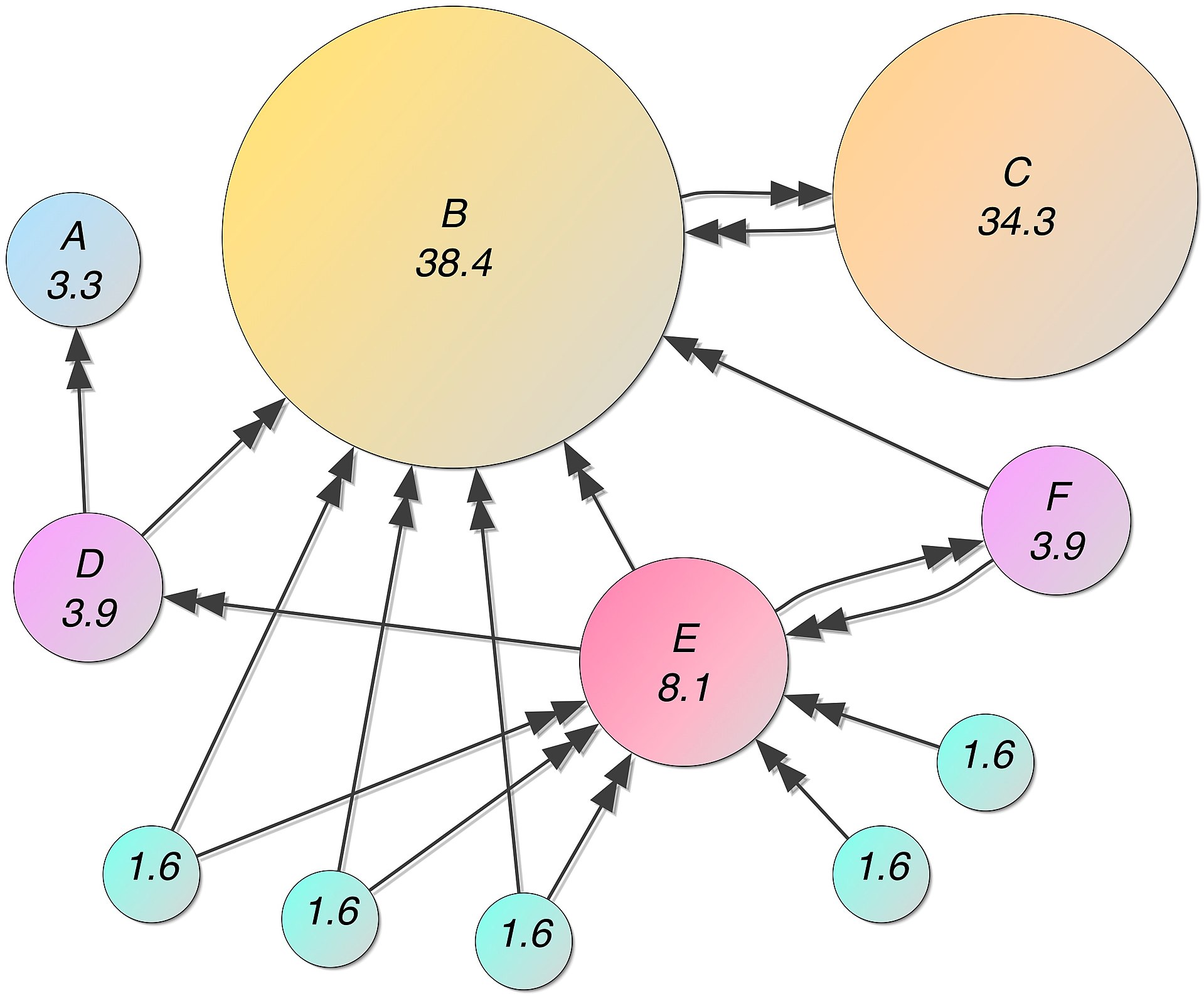
PageRank: scoring#

Imagine a browser doing a random walk
- At time t=0, start at a random webpage.
- At time t=1, follow a random link on the current page.
- At time t=2, follow a random link on the current page.
Intuition
- In the “steady state” each page has a long-term visit rate, which is the page’s score (rank).

PageRank: teleporting#

Obvious problem with the random walk:
- Pages with no in-links have a rank of 0.
- Algorithm can get “stuck” in part of the graph, as the web is full of dead-ends.

PageRank: teleporting#

At a dead end, jump to a random web page.
At a non-dead end, we still jump to a random web page with probability $\alpha$.
With the remaining probability $(1-\alpha)$ go out on a random link.
With teleporting, we cannot get stuck locally.

Questions#

PageRank as a Markov chain#

A state is a web page
Transition probabilities represent probabilities of moving from one page to another
We derive these from the adjacency matrix of the web graph
- Adjacency matrix $M$ is a $n \times n$ matrix, if $n$ is the number of states (web pages)
- $M_{ij} = 1$ if there is a hyperlink from page $i$ to page $j$.

PageRank: deriving transition matrix#

If a state has no out-links, the random surfer teleports:
- the transition probability to each state from this state is $1/n$, if $n$ is the number of states
If a node has K > 0 outgoing links:
- with probability $0 \leq \alpha \leq 1$ the surfer teleports to a random node
  - probability is $\alpha/n$
- with probability $(1-\alpha)$ the surfer takes a normal random walk
  - probability is $(1-\alpha)/K$

PageRank: deriving transition matrix#

If a row has all 0’s, replace each element by $1/n$
Else
- Normalize: divide each 1 by the number of 1’s in the row
- Multiply the resulting matrix by $(1-\alpha)$
- Add $\alpha/n$ to every element in the resulting matrix to create the transition matrix $A$.

PageRank: deriving transition matrix (example)#

Adjacency matrix: $ M =

(17)#\[\begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0\\ \end{bmatrix}\]

, \alpha = 0.0$

Transition matrix: $ A_{\alpha=0} =

(18)#\[\begin{bmatrix} 0 & 1 & 0\\ 0.5 & 0 & 0.5\\ 0 & 1 & 0\\ \end{bmatrix}\]

PageRank: deriving transition matrix (example)#

$ M =

(19)#\[\begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0\\ \end{bmatrix}\]

, n =3, \alpha = 0.5$

Normalize: divide each 1 by the number of 1’s in the row:
$

(20)#\[\begin{bmatrix} 0 & 1 & 0\\ 1/2 & 0 & 1/2\\ 0 & 1 & 0\\ \end{bmatrix}\]

PageRank: deriving transition matrix (example)#

$ M =

(21)#\[\begin{bmatrix} 0 & 1 & 0\\ 1 & 0 & 1\\ 0 & 1 & 0\\ \end{bmatrix}\]

, n =3, \alpha = 0.5$

Normalized
Multiply the resulting matrix by $(1-\alpha)$: $ (1-0.5)

(22)#\[\begin{bmatrix} 0 & 1 & 0\\ 1/2 & 0 & 1/2\\ 0 & 1 & 0\\ \end{bmatrix}\]

$ =

(23)#\[\begin{bmatrix} 0 & 1/2 & 0\\ 1/4 & 0 & 1/4\\ 0 & 1/2 & 0\\ \end{bmatrix}\]

Add $\alpha/n$ to every element in the resulting matrix to create the transition matrix: $ A_{\alpha = 0.5} =

(24)#\[\begin{bmatrix} 1/6 & 2/3 & 1/6\\ 5/12 & 1/6 & 5/12\\ 1/6 & 2/3 & 1/6\\ \end{bmatrix}\]

Questions#

Calculate page rank#

We have a transition matrix: $A_{\alpha = 0.5} =

(25)#\[\begin{bmatrix} 1/6 & 2/3 & 1/6\\ 5/12 & 1/6 & 5/12\\ 1/6 & 2/3 & 1/6\\ \end{bmatrix}\]

We want to find the stationary distribution
- Is it irreducible?
- Is it aperiodic?

Calculate page rank: power iteration method#

Start with a random initial probability distribution $\pi$
Multiply $\pi$ by powers of the transition matrix $A$ until the product looks stable
- After one step, we are at $\pi A$
- After two steps, we are at $\pi A^2$
- After three steps, we are at $\pi A^3$
- Eventually (for a large $k$), $\pi A^k = \pi$

How to do this in Python?#

Use networkx package google_matrix function. Warning: their definition of 𝛼 is opposite from ours.

import networkx as nx
G=nx.Graph()
G.add_node('A')
G.add_node('B')
G.add_node('C')
G.add_edge('A','B')
G.add_edge('B','A')
G.add_edge('B','C')
G.add_edge('C','B')
nx.draw(G, with_labels=True)
plt.show()

../_images/bb84eb0d12a992bfb31ea419e7f13538471d8a0b7c5fa9a6e843bf5808b1a103.png

# Transition matrix for alpha = 0.0
print(nx.google_matrix(G, nodelist=sorted(G.nodes()), alpha=1.0 - 0.0))

[[0.  1.  0. ]
 [0.5 0.  0.5]
 [0.  1.  0. ]]

# Transition matrix for alpha = 0.5
A = nx.google_matrix(G, nodelist=sorted(G.nodes()), alpha = 1.0 - 0.5)
print(A)

[[0.16666667 0.66666667 0.16666667]
 [0.41666667 0.16666667 0.41666667]
 [0.16666667 0.66666667 0.16666667]]

def print_pi_over_time(s0, T, steps=10):
    prev = s0
    print('Step 0', prev)
    for i in range(steps):    
        current = prev@T
        print('Step ', i+1, current)
        prev = current

# Random initialization of pi
pi = [.4, 0.2, 0.2]
# Power iteration method
print_pi_over_time(pi, A, steps=40)

Step 0 [0.4, 0.2, 0.2]
Step  1 [[0.18333333 0.43333333 0.18333333]]
Step  2 [[0.24166667 0.31666667 0.24166667]]
Step  3 [[0.2125 0.375  0.2125]]
Step  4 [[0.22708333 0.34583333 0.22708333]]
Step  5 [[0.21979167 0.36041667 0.21979167]]
Step  6 [[0.2234375 0.353125  0.2234375]]
Step  7 [[0.22161458 0.35677083 0.22161458]]
Step  8 [[0.22252604 0.35494792 0.22252604]]
Step  9 [[0.22207031 0.35585937 0.22207031]]
Step  10 [[0.22229818 0.35540365 0.22229818]]
Step  11 [[0.22218424 0.35563151 0.22218424]]
Step  12 [[0.22224121 0.35551758 0.22224121]]
Step  13 [[0.22221273 0.35557454 0.22221273]]
Step  14 [[0.22222697 0.35554606 0.22222697]]
Step  15 [[0.22221985 0.3555603  0.22221985]]
Step  16 [[0.22222341 0.35555318 0.22222341]]
Step  17 [[0.22222163 0.35555674 0.22222163]]
Step  18 [[0.22222252 0.35555496 0.22222252]]
Step  19 [[0.22222207 0.35555585 0.22222207]]
Step  20 [[0.2222223  0.35555541 0.2222223 ]]
Step  21 [[0.22222219 0.35555563 0.22222219]]
Step  22 [[0.22222224 0.35555552 0.22222224]]
Step  23 [[0.22222221 0.35555557 0.22222221]]
Step  24 [[0.22222223 0.35555555 0.22222223]]
Step  25 [[0.22222222 0.35555556 0.22222222]]
Step  26 [[0.22222222 0.35555555 0.22222222]]
Step  27 [[0.22222222 0.35555556 0.22222222]]
Step  28 [[0.22222222 0.35555555 0.22222222]]
Step  29 [[0.22222222 0.35555556 0.22222222]]
Step  30 [[0.22222222 0.35555556 0.22222222]]
Step  31 [[0.22222222 0.35555556 0.22222222]]
Step  32 [[0.22222222 0.35555556 0.22222222]]
Step  33 [[0.22222222 0.35555556 0.22222222]]
Step  34 [[0.22222222 0.35555556 0.22222222]]
Step  35 [[0.22222222 0.35555556 0.22222222]]
Step  36 [[0.22222222 0.35555556 0.22222222]]
Step  37 [[0.22222222 0.35555556 0.22222222]]
Step  38 [[0.22222222 0.35555556 0.22222222]]
Step  39 [[0.22222222 0.35555556 0.22222222]]
Step  40 [[0.22222222 0.35555556 0.22222222]]

Modern ranking methods are more advanced:#

Guarding against methods that exploit algorithm.
Removing offensive/illegal content.
Supervised and personalized ranking methods.
Take into account that you often only care about top rankings.
Also work on diversity of rankings:
E.g., divide objects into sub-topics and do weighted “covering” of topics.
Persistence/freshness as in recommender systems (news articles).

PageRank as a Markov model

Contents

PageRank as a Markov model#

PageRank: intuition#

PageRank: scoring#

PageRank: teleporting#

PageRank: teleporting#

Questions#

PageRank as a Markov chain#

PageRank: deriving transition matrix#

PageRank: deriving transition matrix#

PageRank: deriving transition matrix (example)#

PageRank: deriving transition matrix (example)#

PageRank: deriving transition matrix (example)#

Questions#

Calculate page rank#

Calculate page rank: power iteration method#

How to do this in Python?#

Modern ranking methods are more advanced:#