Lecture 4 - Linear Mixed-Effects Models

Today’s Learning Goals

By the end of this lecture, you should be able to:

• Identify the model assumptions in a linear Mixed-Effects model.

• Associate a term (or combination of terms) in a Mixed-Effects model with the following quantities:

  • Fixed effect estimates.

  • Variances of the random effects.

  • Regression coefficients for each group and population.

  • Predictions on existing groups and a new group.

• Fit a linear Mixed-Effects model in R, and extract estimates of the above quantities.

• Identify the consequences of fitting a fixed-effects linear regression model when there are groups, whether a slope parameter is pooled or fit separately per group.

• Explain the difference between the distributional assumption on the random effects and the fixed effects estimates’ sampling distribution.

Loading Libraries

options(repr.matrix.max.rows = 6)
library(AER)
library(tidyverse)
library(broom)
library(nlme)
library(lme4)
library(lmerTest)

1. Linear Fixed-Effects Model

So far, we have been working with regression models fitted with a training set of \(n\) independent elements.

Let us start with different modelling techniques from the ones you learned in DSCI 561. Under a frequentist and classical Ordinary Least-squares (OLS) paradigm, given a set of \(k\) regressors \(X_{i,j}\) and a continuous response \(Y_i\), we fit a model

\[Y_i = \beta_0 + \beta_1 X_{i,1} + \beta_2 X_{i,2} + \ldots + \beta_k X_{i,k} + \varepsilon_{i} \; \; \; \; \text{for} \; i = 1, \ldots, n.\]

Note parameters \(\beta_0, \beta_1, \dots, \beta_k\) are fixed and constant for all the observed values \(\left(x_{i,1}, \dots, x_{i,k}, y_i\right)\).

Definition of Fixed Effects

OLS parameters \(\beta_0, \beta_1, \dots, \beta_k\) are called fixed effects in Regression Analysis. In an inferential framework, it is our interest to evaluate whether they are statistically significant for the response.

To illustrate today’s topic, let us introduce a suitable dataset.

1.1. Grunfeld’s Investment Dataset

Consider the following example: to study how gross investment depends on the firm’s value and capital stock, Grunfeld (1958) collected data from eleven different American companies over the years 1935-1954.

The Grunfeld’s Investment Dataset

The data frame Grunfeld, from package AER, contains 220 observations from a balanced panel of 11 sampled American firms from 1935 to 1954 (20 observations per firm). The dataset includes a continuous response investment subject to two explanatory variables, market_value and capital.

Definition of Balanced Panel

In statistical jargon, a panel refers to a dataset in which each individual (e.g., a firm) is observed within a timeframe. Furthermore, the term balanced indicates that we have the same number of observations per individual.

Firstly, we will load the data which has the following variables:

• investment: the gross investment in millions of American dollars (additions to plant and equipment along with maintenance), a continuous response.

• market_value: the firm’s market value in millions of American dollars, a continuous explanatory variable.

• capital: stock of plant and equipment in millions of American dollars, a continuous explanatory variable.

• firm: a nominal explanatory variable with eleven levels indicating the firm (General Motors, US Steel, General Electric, Chrysler, Atlantic Refining, IBM, Union Oil, Westinghouse, Goodyear, Diamond Match, and American Steel).

• year: the year of the observation (it will not be used in our analysis, but take it into account for our next in-class question).

The code below only renames some columns from the original dataset.

data(Grunfeld)
Grunfeld <- Grunfeld %>% 
  rename(investment = invest, market_value = value)
Grunfeld

A data.frame: 220 × 5

	investment	market_value	capital	firm	year
	<dbl>	<dbl>	<dbl>	<fct>	<int>
1	317.6	3078.5	2.8	General Motors	1935
2	391.8	4661.7	52.6	General Motors	1936
3	410.6	5387.1	156.9	General Motors	1937
⋮	⋮	⋮	⋮	⋮	⋮
218	7.329	57.616	78.631	American Steel	1952
219	9.020	57.441	80.215	American Steel	1953
220	6.281	47.165	83.788	American Steel	1954

We will start with an in-class question via iClicker.

Exercise 12

What class of data hierarchy do you observe in this dataset? Do you expect any class of correlation within the data points?

A. Yes, we have a data hierarchy with one level: firm. Still, there will not be a correlation among subsets of data points.

B. Yes, we have a data hierarchy with one level: firm. Hence, there will be a correlation among subsets of data points.

C. There is no data hierarchy at all. All observations in the training set are independent.

D. Yes, we have a data hierarchy with two levels: firm (level 1) and the corresponding yearly observations (level 2). Hence, there will be a correlation among subsets of data points.

Main Statistical Inquiries

We are interested in assessing the association of gross investment with market_value and capital in the population of American firms. Then, how can we fit a linear model to this data?

1.2. Exploratory Data Analysis

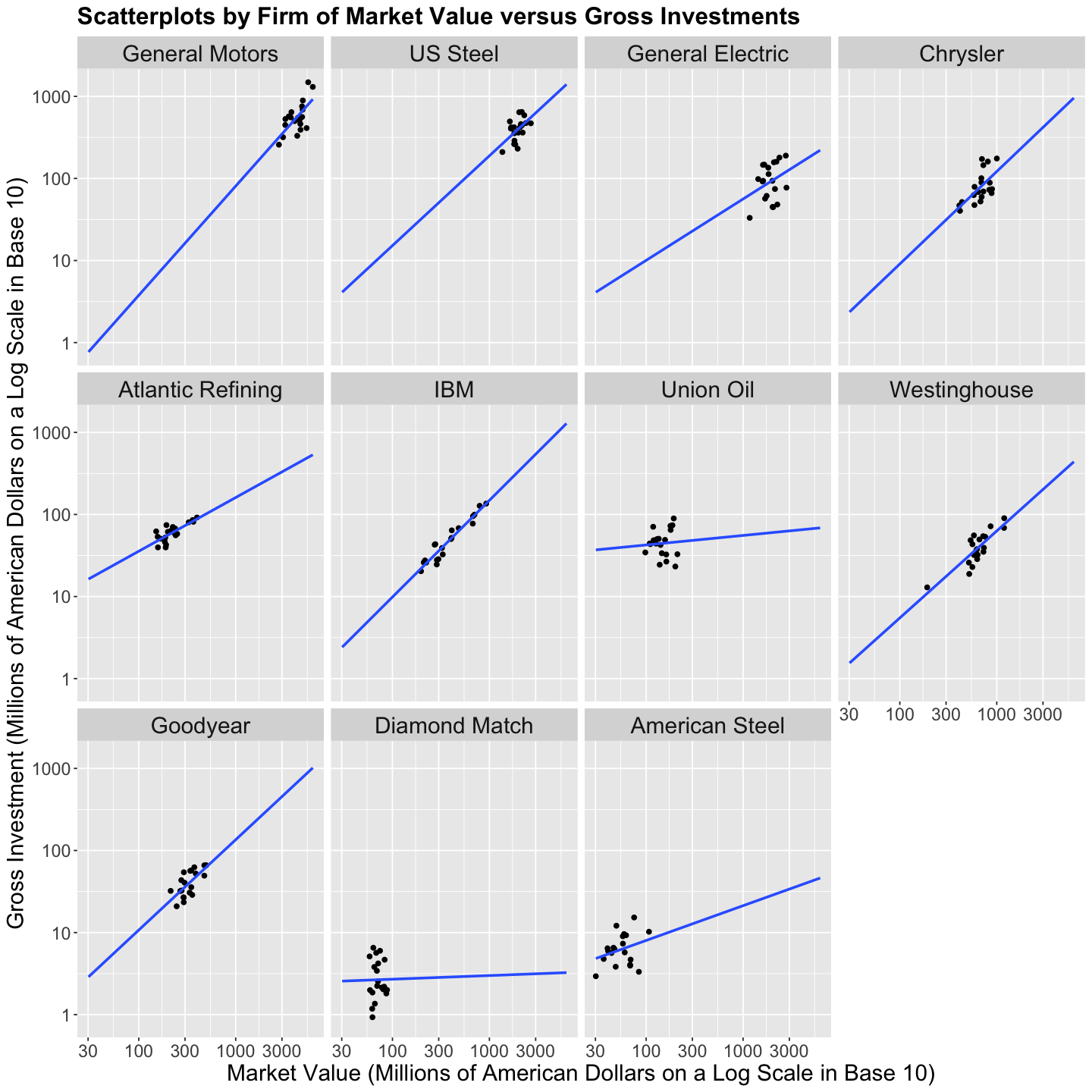
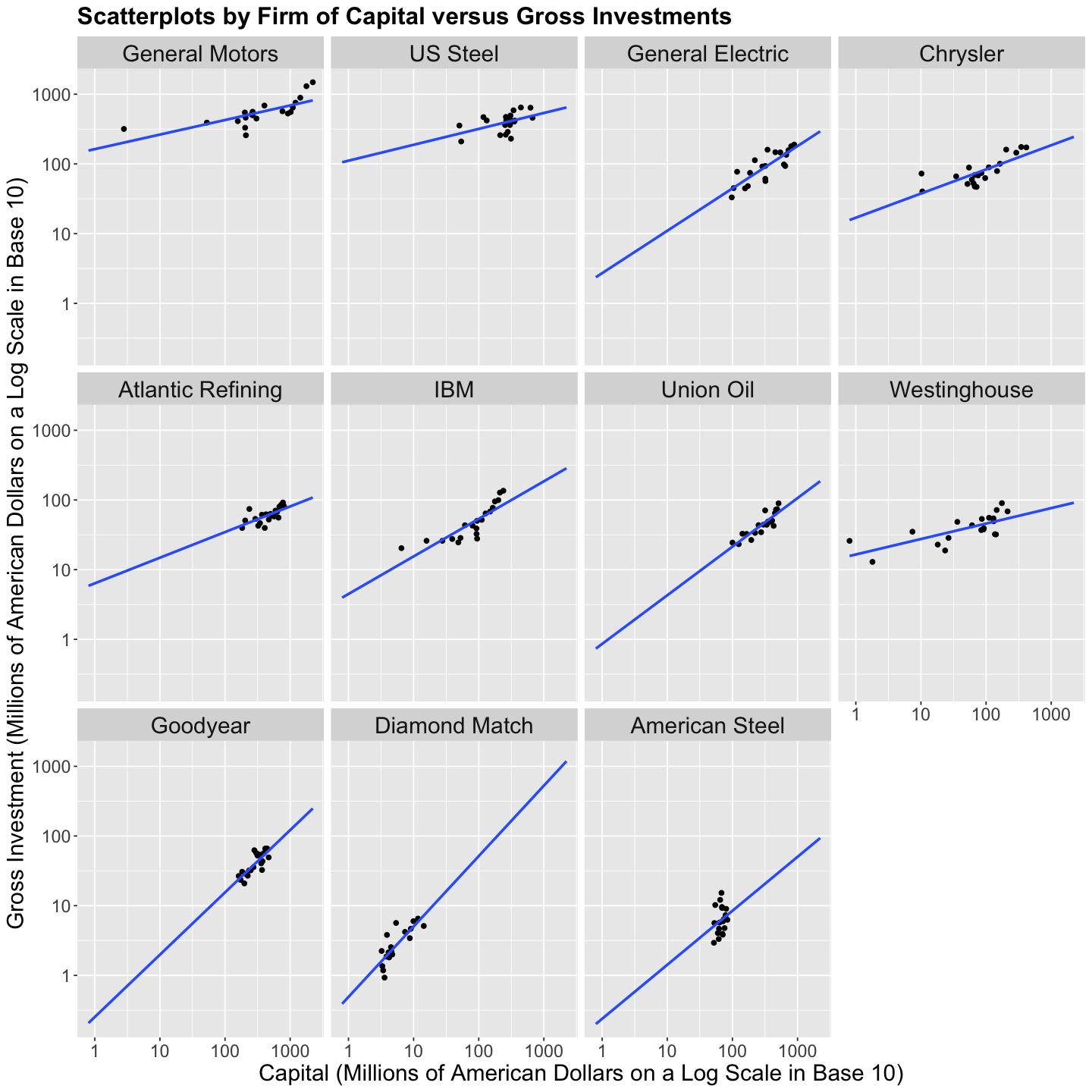
Let us plot the \(n = 220\) data points of investment versus market_value and capital but facetted by firm and use geom_smooth() to fit sub-models by firm.

Important

Only for plotting, we will transform both \(x\) and \(y\)-axes on the logarithmic scale in base 10 (trans = "log10"). This allows us to compare those firms under dissimilar market values, capital, and gross investments.

scatterplots_firm_market_value <- Grunfeld %>%
  ggplot(aes(market_value, investment)) +
  geom_point() +
  geom_smooth(method = "lm", fullrange = TRUE, formula = y ~ x, se = FALSE) +
  facet_wrap(~firm) +
  labs(x = "Market Value (Millions of American Dollars on a Log Scale in Base 10)", 
       y = "Gross Investment (Millions of American Dollars on a Log Scale in Base 10)") +
  ggtitle("Scatterplots by Firm of Market Value versus Gross Investments") +
  theme(
    plot.title = element_text(size = 25, face = "bold"),
    axis.text = element_text(size = 16),
    axis.title = element_text(size = 22),
    strip.text.x = element_text(size = 22),
  ) +
  scale_x_continuous(trans = "log10") +
  scale_y_continuous(trans = "log10")

scatterplots_firm_capital <- Grunfeld %>%
  ggplot(aes(capital, investment)) +
  geom_point() +
  geom_smooth(method = "lm", fullrange = TRUE, formula = y ~ x, se = FALSE) +
  facet_wrap(~firm) +
  labs(x = "Capital (Millions of American Dollars on a Log Scale in Base 10)", 
       y = "Gross Investment (Millions of American Dollars on a Log Scale in Base 10)") +
  ggtitle("Scatterplots by Firm of Capital versus Gross Investments") +
  theme(
    plot.title = element_text(size = 25, face = "bold"),
    axis.text = element_text(size = 16),
    axis.title = element_text(size = 22),
    strip.text.x = element_text(size = 22),
  ) +
  scale_x_continuous(trans = "log10") +
  scale_y_continuous(trans = "log10")

options(repr.plot.height = 12.5, repr.plot.width = 14.5)

scatterplots_firm_market_value

scatterplots_firm_capital

Exercise 13

What do you observe in the plots above?

1.3. OLS Modelling Framework

Before digging into today’s new modelling approach, let us try a classical approach via OLS for comparative purposes.

Warning

Always keep in mind the main statistical inquiry when taking any given modelling approach.

1.3.1. Regression Alternatives

Based on what you have seen via OLS in DSCI 561, there might be four possible approaches:

• Take the average for each firm, and fit an OLS regression on the averages. This is not an ideal approach, since we would lose valuable data points if we summarize them using a summary statistic of central tendency such as the average. Recall the frequentist paradigm: the more data points, the better! Therefore, we will not use this approach in this lecture.

• We could ignore firm, and fit an OLS regression with the other columns in the training set. Nonetheless, this is not an ideal approach since we will not be properly defining the corresponding systematic component of our population of interest: American firms.

• Allow different intercepts for each firm. This might be an approach worth taking using OLS modelling techniques.

• Allow a different slope and intercept for each firm (i.e., and interaction model!). This might be an approach worth taking using OLS modelling techniques.

1.3.2. OLS Ignoring Firm

Let us start with this basic OLS model to warm up our modelling skills regarding setting up equations. Suppose we ignore factor firm. Then, we will estimate an OLS regression with investment as a response to market_value and capital as regressors.

The regression equation for the \(i\)th sampled observation will be:

\[\texttt{investment}_{i} = \beta_0 + \beta_1 \texttt{marketValue}_{i} + \beta_2\texttt{capital}_{i} + \varepsilon_{i} \; \; \; \; \text{for} \; i = 1, \ldots, 220.\]

We use lm() and glance() to get the corresponding outputs.

ordinary_model <- lm(formula = investment ~ market_value + capital, data = Grunfeld)
tidy(ordinary_model) %>%
  mutate_if(is.numeric, round, 4)
glance(ordinary_model) %>%
  mutate_if(is.numeric, round, 4)

A tibble: 3 × 5

term	estimate	std.error	statistic	p.value
<chr>	<dbl>	<dbl>	<dbl>	<dbl>
(Intercept)	-38.4101	8.4134	-4.5654	0
market_value	0.1145	0.0055	20.7534	0
capital	0.2275	0.0242	9.3904	0

A tibble: 1 × 12

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual	nobs
<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
0.8179	0.8162	90.2806	487.284	0	2	-1301.299	2610.598	2624.173	1768678	217	220

With \(\alpha = 0.05\), we have evidence to state see that market_value and capital are statistically associated to investment since the \(p\text{-values} < .001\).

1.3.3. OLS Regression with Varying Intercept

Now, let us estimate another OLS regression model with investment as a response to market_value and capital as regressors but with varying intercepts by each firm.

We will do this with the lm() function by adding - 1 on the right-hand side of the argument formula. This - 1 will allow the baseline firm to have its intercept (i.e., renaming (Intercept) in column estimate with firmCompanyName). In this case, General Motors is the baseline (it appears on the left-had side of the levels() output).

levels(Grunfeld$firm)

1. 'General Motors'
2. 'US Steel'
3. 'General Electric'
4. 'Chrysler'
5. 'Atlantic Refining'
6. 'IBM'
7. 'Union Oil'
8. 'Westinghouse'
9. 'Goodyear'
10. 'Diamond Match'
11. 'American Steel'

options(repr.matrix.max.rows = 33)

model_varying_intercept <- lm(formula = investment ~ market_value + capital + firm - 1, data = Grunfeld)
tidy(model_varying_intercept) %>%
  mutate_if(is.numeric, round, 4)
glance(model_varying_intercept) %>%
  mutate_if(is.numeric, round, 4) 

A tibble: 13 × 5

term	estimate	std.error	statistic	p.value
<chr>	<dbl>	<dbl>	<dbl>	<dbl>
market_value	0.1101	0.0113	9.7461	0.0000
capital	0.3100	0.0165	18.7439	0.0000
firmGeneral Motors	-70.2991	47.3754	-1.4839	0.1394
firmUS Steel	101.9047	23.7687	4.2873	0.0000
firmGeneral Electric	-235.5694	23.2861	-10.1163	0.0000
firmChrysler	-27.8091	13.4186	-2.0724	0.0395
firmAtlantic Refining	-114.6025	13.5025	-8.4875	0.0000
firmIBM	-23.1602	12.0759	-1.9179	0.0565
firmUnion Oil	-66.5442	12.2420	-5.4357	0.0000
firmWestinghouse	-57.5465	13.3379	-4.3145	0.0000
firmGoodyear	-87.2145	12.2887	-7.0971	0.0000
firmDiamond Match	-6.5680	11.2736	-0.5826	0.5608
firmAmerican Steel	-20.5782	11.2978	-1.8214	0.0700

A tibble: 1 × 12

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual	nobs
<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
0.9616	0.9591	50.2995	398.2336	0	13	-1167.426	2362.851	2410.362	523718.7	207	220

By checking the adj.r.squared, we see that model_varying_intercept has a larger value (0.96) than ordinary_model (0.82) (i.e., the first fitted model without firm as a regressor). This indicates that a model with estimated intercepts by firm fits the data better than a model without taking firm into account (at least by looking at the metrics!).

Note that model_varying_intercept is equivalent to just fitting the OLS model using formula = investment ~ market_value + capital + firm. However, in this primary_OLS, General Motors estimated intercept would be called (Intercept) whereas the remaining ten firms will have their corresponding estimated intercepts as (Intercept) + firmCompany as in the primary_OLS. Moreover, the regression parameter estimates for market_value and capital (along with their corresponding standard errors, test statistics, and \(p\text{-values}\)) stay the same.

Caution

Even though the intercept estimates by firm can be easily computed using column estimate from primary_OLS; standard errors, test statistics, and \(p\text{-values}\) will be different given the model parametrization in the regression equation.

primary_OLS <- lm(investment ~ market_value + capital + firm , data = Grunfeld)
tidy(primary_OLS) %>%
  mutate_if(is.numeric, round, 4) 

A tibble: 13 × 5

term	estimate	std.error	statistic	p.value
<chr>	<dbl>	<dbl>	<dbl>	<dbl>
(Intercept)	-70.2991	47.3754	-1.4839	0.1394
market_value	0.1101	0.0113	9.7461	0.0000
capital	0.3100	0.0165	18.7439	0.0000
firmUS Steel	172.2038	29.7001	5.7981	0.0000
firmGeneral Electric	-165.2703	30.2853	-5.4571	0.0000
firmChrysler	42.4900	41.8499	1.0153	0.3112
firmAtlantic Refining	-44.3034	48.1222	-0.9206	0.3583
firmIBM	47.1389	44.6144	1.0566	0.2919
firmUnion Oil	3.7548	48.1918	0.0779	0.9380
firmWestinghouse	12.7526	41.9860	0.3037	0.7616
firmGoodyear	-16.9155	46.1794	-0.3663	0.7145
firmDiamond Match	63.7310	47.9689	1.3286	0.1854
firmAmerican Steel	49.7209	48.2801	1.0298	0.3043

Going back to model_varying_intercept and ordinary_model, we can test if there is a gain in considering a varying intercept versus fixed intercept. Hence, we will make a formal \(F\)-test to check whether the model_varying_intercept fits the data better than the ordinary_model.

anova(ordinary_model, model_varying_intercept) %>%
  mutate_if(is.numeric, round, 2) 

A anova: 2 × 6

	Res.Df	RSS	Df	Sum of Sq	F	Pr(>F)
	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
1	217	1768678.4	NA	NA	NA	NA
2	207	523718.7	10	1244960	49.21	0

We obtain a \(p\text{-value} < .001\). Thus, with \(\alpha = 0.05\), we have evidence to conclude that model_varying_intercept fits the data better than the ordinary_model.

However, this costs us one extra degree of freedom per firm except for the baseline. Therefore, we lose another 10 degrees of freedom (column DF in the anova() output).

Important

In this case, losing 10 degrees of freedom is not a big deal with 220 data points. Nonetheless, in other cases, when data is scarce, this could be an issue regarding inferential inquiries since we need them to perform the corresponding hypothesis testing.

Exercise 14

What is the sample’s regression equation for model_varying_intercept?

A.

\[\begin{split}\begin{align*} \texttt{investment}_{i,j} &= \beta_{0} + \beta_1 \texttt{marketValue}_{i,j} + \beta_2\texttt{capital}_{i,j} + \varepsilon_{i,j} \\ & \qquad \qquad \quad \text{for} \; i = 1, \ldots, 20 \; \; \text{and} \; \; j = 1, \ldots, 11. \end{align*}\end{split}\]

B.

\[\begin{split}\begin{align*} \texttt{investment}_{i} &= \beta_{0} + \beta_1 \texttt{marketValue}_{i} + \beta_2\texttt{capital}_{i} + \varepsilon_{i} \\ & \qquad \qquad \quad \text{for} \; i = 1, \ldots, 220. \end{align*}\end{split}\]

C.

\[\begin{split}\begin{align*} \texttt{investment}_{i,j} &= \beta_{0,j} + \beta_1 \texttt{marketValue}_{i,j} + \beta_2\texttt{capital}_{i,j} + \varepsilon_{i,j} \\ & \qquad \qquad \quad \text{for} \; i = 1, \ldots, 20 \; \; \text{and} \; \; j = 1, \ldots, 11. \end{align*}\end{split}\]

1.3.4. OLS Regression for Each Firm

We can make the model more complex with two interactions (market_value * firm and capital * firm). This will estimate a linear regression by firm with its own slopes.

model_by_firm <- lm(investment ~ market_value * firm + capital * firm, data = Grunfeld)
tidy(model_by_firm) %>%
  mutate_if(is.numeric, round, 2)
glance(model_by_firm) %>%
  mutate_if(is.numeric, round, 2)

A tibble: 33 × 5

term	estimate	std.error	statistic	p.value
<chr>	<dbl>	<dbl>	<dbl>	<dbl>
(Intercept)	-149.78	48.07	-3.12	0.00
market_value	0.12	0.01	10.17	0.00
firmUS Steel	100.58	80.04	1.26	0.21
firmGeneral Electric	139.83	67.16	2.08	0.04
firmChrysler	143.59	64.09	2.24	0.03
firmAtlantic Refining	172.49	57.52	3.00	0.00
firmIBM	141.10	53.48	2.64	0.01
firmUnion Oil	145.28	69.34	2.10	0.04
firmWestinghouse	149.27	58.14	2.57	0.01
firmGoodyear	142.06	64.41	2.21	0.03
firmDiamond Match	149.94	92.75	1.62	0.11
firmAmerican Steel	147.14	102.37	1.44	0.15
capital	0.37	0.02	22.06	0.00
market_value:firmUS Steel	0.06	0.03	1.63	0.11
market_value:firmGeneral Electric	-0.09	0.03	-3.56	0.00
market_value:firmChrysler	-0.04	0.06	-0.65	0.52
market_value:firmAtlantic Refining	0.04	0.26	0.16	0.87
market_value:firmIBM	0.01	0.16	0.08	0.94
market_value:firmUnion Oil	-0.03	0.29	-0.11	0.91
market_value:firmWestinghouse	-0.07	0.07	-1.02	0.31
market_value:firmGoodyear	-0.04	0.16	-0.28	0.78
market_value:firmDiamond Match	-0.11	1.04	-0.11	0.91
market_value:firmAmerican Steel	-0.05	0.55	-0.10	0.92
firmUS Steel:capital	0.02	0.06	0.29	0.78
firmGeneral Electric:capital	-0.22	0.04	-5.24	0.00
firmChrysler:capital	-0.06	0.09	-0.61	0.55
firmAtlantic Refining:capital	-0.37	0.10	-3.60	0.00
firmIBM:capital	-0.29	0.52	-0.55	0.58
firmUnion Oil:capital	-0.25	0.08	-3.20	0.00
firmWestinghouse:capital	-0.28	0.23	-1.22	0.23
firmGoodyear:capital	-0.29	0.13	-2.24	0.03
firmDiamond Match:capital	0.07	3.06	0.02	0.98
firmAmerican Steel:capital	-0.29	1.10	-0.26	0.79

A tibble: 1 × 12

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual	nobs
<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
0.97	0.96	41.68	168.84	0	32	-1114.91	2297.81	2413.2	324895.6	187	220

In this case, we are fitting eleven linear regressions, each with 20 points.

Important

We have plenty of data points in this case for all the degrees of freedom required to estimate each parameter. Nonetheless, this might not be the case with other datasets.

Exercise 15

What is the sample’s regression equation for model_by_firm?

A.

\[\begin{split}\begin{align*} \texttt{investment}_{i,j} &= \beta_{0,j} + \beta_{1,j} \texttt{marketValue}_{i,j} + \beta_{2,j} \texttt{capital}_{i,j} + \varepsilon_{i,j} \\ & \qquad \qquad \quad \text{for} \; i = 1, \ldots, 20 \; \; \text{and} \; \; j = 1, \ldots, 11. \end{align*}\end{split}\]

B.

\[\begin{split}\begin{align*} \texttt{investment}_{j} &= \beta_{0} + \beta_1 \texttt{marketValue}_{j} + \beta_2\texttt{capital}_{j} + \varepsilon_{j} \\ & \qquad \qquad \quad \text{for} \; j = 1, \ldots, 11. \end{align*}\end{split}\]

C.

\[\begin{split}\begin{align*} \texttt{investment}_{i,j} &= \beta_{0,i} + \beta_{1,i} \texttt{marketValue}_{i,j} + \beta_{2,i} \texttt{capital}_{i,j} + \varepsilon_{i,j} \\ & \qquad \qquad \quad \text{for} \; i = 1, \ldots, 20 \; \; \text{and} \; \; j = 1, \ldots, 11. \end{align*}\end{split}\]

We went as far as fitting a separate linear regression for each firm.

How to interpret the coefficients in this model?

Each regression coefficient is associated with a firm. For example, \(\texttt{firmUS Steel:capital} = 0.02\) means that the variable capital has a slope of \(0.02 + 0.37 = 0.39\) for US Steel. We can double-check this by estimating an individual linear regression for US Steel:

tidy(lm(investment ~ market_value + capital, data = Grunfeld %>% filter(firm == "US Steel"))) %>%
  mutate_if(is.numeric, round, 2)

A tibble: 3 × 5

term	estimate	std.error	statistic	p.value
<chr>	<dbl>	<dbl>	<dbl>	<dbl>
(Intercept)	-49.20	148.08	-0.33	0.74
market_value	0.17	0.07	2.36	0.03
capital	0.39	0.14	2.74	0.01

Exercise 16

Now, after all these OLS modelling approaches, are we in line with the main modelling objective with all these linear regression models?

Fig. 10 The Questioning Panda, again!

2. Linear Mixed-Effects Model

The fact that we have a sample of 11 companies and our inquiry aims to make inference on the population of American companies, along with the correlated data structure in this panel, paves the way to linear Mixed-Effects modelling.

Important

In linear Mixed-Effects modelling, the \(n\) rows in our training set will not be independent anymore. Let us view it this way: possibly, your data subsets of elements share a correlation structure (e.g., observations over time on a given response and regressors for a specific subject in a panel). This is the fundamental idea in Mixed-Effects regression.

Let us take a step back and think about a population of companies. For instance, all American companies. Grunfeld did not collect data on all the American companies but sampled 11 companies from this population. The author was interested in assessing whether market_value and capital were related to investment and by how much.

Let us assume that the \(j\)th sampled firm has its own intercept \(b_{0,j}\) and the overall fixed intercept is \(\beta_0\) for all American companies. Therefore, for the \(j\)th firm, we define the following mixed intercept:

\[ \beta_{0,j} = \beta_0 + b_{0,j}. \]

The intercept \(b_{0,j}\) is specifically for the \(j\)th firm that was sampled. It will change due to chance since it is linked to the \(j\)th sampled firm which would make it a random effect. This is the deviation of the \(j\)th firm from the overall fixed intercept \(\beta_0\).

The regression paradigm of estimating a fixed unknown intercept \(\beta_0\) will change now. Moreover, the intercept \(\beta_{0,j}\) is what we call a mixed effect:

\[\begin{split}\begin{align*} \texttt{investment}_{i,j} &= \overbrace{\beta_{0,j}}^{\text{Mixed Effect}} + \beta_1 \texttt{marketValue}_{i,j} + \beta_2\texttt{capital}_{i,j} + \varepsilon_{i,j} \\ &= (\beta_0 + b_{0,j}) + \beta_1 \texttt{marketValue}_{i,j} + \beta_2\texttt{capital}_{i,j} + \varepsilon_{i,j} \\ & \qquad \qquad \qquad \; \; \; \; \text{for} \; i = 1, \ldots, n_j \; \; \text{and} \; \; j = 1, \ldots, 11. \end{align*}\end{split}\]

Note that \(n_j\) is making the model even more flexible by allowing different numbers of observations \(n_j\) in each \(j\)th firm.

Now,

\[b_{0,j}\sim \mathcal{N}(0, \sigma_0^2)\]

is called a random effect and we assume it is independent of the error component

\[\varepsilon_{i,j}\sim \mathcal{N}(0, \sigma^2).\]

The observations for the same firm (group) share the same random effect making a correlation structure.

The variance of the \(i\)th response for the \(j\)th firm will be

\[ \text{Var}(\texttt{investment}_{i,j}) = \text{Var}(b_{0,j}) + \text{Var}(\varepsilon_{i,j}) = \sigma_0^2 + \sigma^2. \]

For the \(k\)th and \(l\)th responses, within the \(j\)th firm, the correlation is given by:

\[ \text{Corr}(\texttt{investment}_{k,j}, \texttt{investment}_{l,j}) = \frac{\sigma^2_0}{\sigma_0^2 + \sigma^2}. \]

We could even go further and model random slopes, along with the existing fixed ones, as follows:

\[\begin{split}\begin{align*} \texttt{investment}_{i,j} &= \overbrace{\beta_{0,j}}^{\text{Mixed Effect}} + \overbrace{\beta_{1,j}}^{\text{Mixed Effect}} \times \texttt{marketValue}_{i,j} + \overbrace{\beta_{2,j}}^{\text{Mixed Effect}} \times \texttt{capital}_{i,j} + \varepsilon_{i,j} \\ &= (\beta_0 + b_{0,j}) + (\beta_1 + b_{1,j}) \times \texttt{marketValue}_{i,j} + (\beta_2 + b_{2,j}) \times \texttt{capital}_{i,j} + \varepsilon_{i,j} \\ & \qquad \qquad \qquad \qquad \qquad \qquad \text{for} \; i = 1, \ldots, n_j \; \; \text{and} \; \; j = 1, \ldots, 11; \end{align*}\end{split}\]

with \((b_{0,j}, b_{1,j}, b_{2,j})^{T} \sim \mathcal{N}_3(\mathbf{0}, \mathbf{D})\), where \(\mathbf{0} = (0, 0, 0)^T\) and \(\mathbf{D}\) is a generic covariance matrix.

Important

Note that the above random effects \(b_{0,j}\), \(b_{1,j}\), and \(b_{2,j}\) have a Multivariate Gaussian distribution of \(d = 3\). You can review further details about this distribution in the DSCI 551 notes.

2.1. What is this Generic Covariance Matrix \(\mathbf{D}\)?

This is a standard form in linear Mixed-Effects modelling. Hence, this matrix becomes:

\[\begin{split}\begin{equation*} \mathbf{D} = \begin{bmatrix} \sigma_{0}^2 & \rho_{01} \sigma_{0} \sigma_{1} & \rho_{02} \sigma_{0} \sigma_{2}\\ \rho_{01} \sigma_{0} \sigma_{1} & \sigma_{1}^2 & \rho_{12} \sigma_{1} \sigma_{2}\\ \rho_{02} \sigma_{0} \sigma_{2} & \rho_{12} \sigma_{1} \sigma_{2} & \sigma_{2}^2 \end{bmatrix} = \begin{bmatrix} \sigma_{0}^2 & \sigma_{0, 1} & \sigma_{0, 2} \\ \sigma_{0, 1} & \sigma_{1}^2 & \sigma_{1,2}\\ \sigma_{0, 2} & \sigma_{1, 2} & \sigma_{2}^2 \end{bmatrix}, \end{equation*}\end{split}\]

where \(\sigma_{0}^2\), \(\sigma_{1}^2\), and \(\sigma_{2}^2\) are the variances of \(b_{0,j}\), \(b_{1,j}\), and \(b_{2,j}\) respectively.

Moreover \(\rho_{uv} \in [0,1]\) is the correlation between the \(u\)th and the \(v\)th random effects. We can reexpress the covariances as \(\sigma_{u, v}\).

Important

• \(\rho_{uv}\) indicates a Pearson’s correlation, which you can also review here.

• While the random effects are assumed to follow a joint Normal distribution, this is different from the sampling distribution of the estimates of the fixed effects.

• The joint Normal distribution explains the variability of random regression intercepts and coefficients. The spread does not change when we collect more data.

• The sampling distribution explains the uncertainty in the fixed regression estimates and gets narrower as we collect more data.

2.2. Model Fitting, Inference, and Coefficient Interpretation

Let us estimate the regression model with a mixed intercept only (mixed_intercept_model) via the function lmer() from package lme4. Note that (1 | firm) allows the model to have a random intercept by firm.

suppressWarnings(suppressMessages(print(mixed_intercept_model <- lmer(investment ~ market_value +
  capital + (1 | firm),
data = Grunfeld
))))

Linear mixed model fit by REML ['lmerModLmerTest']
Formula: investment ~ market_value + capital + (1 | firm)
   Data: Grunfeld
REML criterion at convergence: 2394.616
Random effects:
 Groups   Name        Std.Dev.
 firm     (Intercept) 82.10   
 Residual             50.27   
Number of obs: 220, groups:  firm, 11
Fixed Effects:
 (Intercept)  market_value       capital  
    -54.0318        0.1094        0.3082  
fit warnings:
Some predictor variables are on very different scales: consider rescaling

Recall the regression equation for mixed_intercept_model:

\[\begin{split}\begin{align*} \texttt{investment}_{i,j} &= \overbrace{\beta_{0,j}}^{\text{Mixed Effect}} + \beta_1 \texttt{marketValue}_{i,j} + \beta_2\texttt{capital}_{i,j} + \varepsilon_{i,j} \\ &= (\beta_0 + b_{0,j}) + \beta_1 \texttt{marketValue}_{i,j} + \beta_2\texttt{capital}_{i,j} + \varepsilon_{i,j} \\ & \qquad \qquad \qquad \; \; \; \; \text{for} \; i = 1, \ldots, n_j \; \; \text{and} \; \; j = 1, \ldots, 11; \end{align*}\end{split}\]

where

\[b_{0,j}\sim \mathcal{N}(0, \sigma_0^2)\]

and

\[\varepsilon_{i,j}\sim \mathcal{N}(0, \sigma^2).\]

The section Random effects will show the estimated standard deviations \(\hat{\sigma}_0\) and \(\hat{\sigma}\) as 82.10 and 50.27, respectively. Estimated Fixed effects \(\hat{\beta}_0\), \(\hat{\beta}_1\), and \(\hat{\beta}_2\) are -54.0318, 0.1094, and 0.3082 respectively.

Now, let us estimate the Mixed-Effects regression model with mixed intercept and slopes (full_mixed_model). Note that (market_value + capital | firm) allows the model to have a random intercept and slopes by firm.

suppressWarnings(suppressMessages(print(full_mixed_model <- lmer(investment ~ market_value +
  capital + (market_value + capital | firm),
data = Grunfeld
))))

Linear mixed model fit by REML ['lmerModLmerTest']
Formula: investment ~ market_value + capital + (market_value + capital |  
    firm)
   Data: Grunfeld
REML criterion at convergence: 2299.116
Random effects:
 Groups   Name         Std.Dev. Corr       
 firm     (Intercept)  15.15612            
          market_value  0.05235 -1.00      
          capital       0.12291 -0.85  0.85
 Residual              40.77647            
Number of obs: 220, groups:  firm, 11
Fixed Effects:
 (Intercept)  market_value       capital  
    -7.79756       0.06118       0.22694  
fit warnings:
Some predictor variables are on very different scales: consider rescaling
optimizer (nloptwrap) convergence code: 0 (OK) ; 0 optimizer warnings; 1 lme4 warnings 

Recall the regression equation for full_mixed_model:

\[\begin{split}\begin{align*} \texttt{investment}_{i,j} &= \overbrace{\beta_{0,j}}^{\text{Mixed Effect}} + \overbrace{\beta_{1,j}}^{\text{Mixed Effect}} \times \texttt{marketValue}_{i,j} + \overbrace{\beta_{2,j}}^{\text{Mixed Effect}} \times \texttt{capital}_{i,j} + \varepsilon_{i,j} \\ &= (\beta_0 + b_{0,j}) + (\beta_1 + b_{1,j}) \times \texttt{marketValue}_{i,j} + (\beta_2 + b_{2,j}) \times \texttt{capital}_{i,j} + \varepsilon_{i,j} \\ & \qquad \qquad \qquad \qquad \qquad \qquad \text{for} \; i = 1, \ldots, n_j \; \; \text{and} \; \; j = 1, \ldots, 11; \end{align*}\end{split}\]

with \((b_{0,j}, b_{1,j}, b_{2,j})^{T} \sim \mathcal{N}_3(\mathbf{0}, \mathbf{D})\), where \(\mathbf{0} = (0, 0, 0)^T\) and \(\mathbf{D}\) is a generic covariance matrix.

The section Random effects will show the estimated standard deviations \(\hat{\sigma}_0\), \(\hat{\sigma}_1\), \(\hat{\sigma}_2\), and \(\hat{\sigma}\) as 15.15612, 0.05235, 0.12291, and 40.77647 respectively. Estimated Fixed effects \(\hat{\beta}_0\), \(\hat{\beta}_1\), and \(\hat{\beta}_2\) are -7.79756, 0.06118, and 0.22694 respectively.

Let us proceed with inference using mixed_intercept_model. We now assess whether the fixed effects are statistically associated with investment in each model via summary(). We will use the package lmerTest along with function summary().

library(lmerTest)
summary(mixed_intercept_model)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: investment ~ market_value + capital + (1 | firm)
   Data: Grunfeld

REML criterion at convergence: 2394.6

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-3.6018 -0.3138  0.0139  0.3148  5.0604 

Random effects:
 Groups   Name        Variance Std.Dev.
 firm     (Intercept) 6741     82.10   
 Residual             2528     50.27   
Number of obs: 220, groups:  firm, 11

Fixed effects:
               Estimate Std. Error         df t value Pr(>|t|)    
(Intercept)  -54.031821  26.623551  12.069048  -2.029   0.0651 .  
market_value   0.109352   0.009987 129.346325  10.950   <2e-16 ***
capital        0.308200   0.016368 213.247094  18.830   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
            (Intr) mrkt_v
market_valu -0.312       
capital     -0.021 -0.369
fit warnings:
Some predictor variables are on very different scales: consider rescaling

We do the same with full_mixed_model.

summary(full_mixed_model)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: investment ~ market_value + capital + (market_value + capital |  
    firm)
   Data: Grunfeld

REML criterion at convergence: 2299.1

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-4.5030 -0.1660  0.0100  0.1819  4.1389 

Random effects:
 Groups   Name         Variance  Std.Dev. Corr       
 firm     (Intercept)  2.297e+02 15.15612            
          market_value 2.741e-03  0.05235 -1.00      
          capital      1.511e-02  0.12291 -0.85  0.85
 Residual              1.663e+03 40.77647            
Number of obs: 220, groups:  firm, 11

Fixed effects:
             Estimate Std. Error       df t value Pr(>|t|)    
(Intercept)  -7.79756    7.79890  7.01489  -1.000 0.350626    
market_value  0.06118    0.01927  7.74466   3.175 0.013660 *  
capital       0.22694    0.04422  9.52493   5.132 0.000517 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
            (Intr) mrkt_v
market_valu -0.691       
capital     -0.547  0.564
fit warnings:
Some predictor variables are on very different scales: consider rescaling
optimizer (nloptwrap) convergence code: 0 (OK)
boundary (singular) fit: see help('isSingular')

We can see that market_value and capital are significant with \(\alpha = 0.05\) in both models. Moreover, the regression coefficients’ interpretation for the fixed effects will be on the effect these regressors have on the population investment mean of the American companies.

We can obtain the estimated coefficients by firm along with the intercepts for both models via coef().

coef(mixed_intercept_model)$firm

A data.frame: 11 × 3

	(Intercept)	market_value	capital
	<dbl>	<dbl>	<dbl>
General Motors	-65.526515	0.109352	0.3081997
US Steel	101.069974	0.109352	0.3081997
General Electric	-230.027388	0.109352	0.3081997
Chrysler	-27.544640	0.109352	0.3081997
Atlantic Refining	-112.435102	0.109352	0.3081997
IBM	-23.220327	0.109352	0.3081997
Union Oil	-65.632801	0.109352	0.3081997
Westinghouse	-56.815866	0.109352	0.3081997
Goodyear	-85.813152	0.109352	0.3081997
Diamond Match	-7.376705	0.109352	0.3081997
American Steel	-21.027505	0.109352	0.3081997

Column (Intercept) is the sum \(\hat{\beta}_0 + \hat{b}_{0,j}\). Note the estimated regression coefficients for market_value and capital are the same since mixed_intercept_model only has \(\beta_1\) and \(\beta_2\) as its general modelling setup.

The coefficient summary changes in full_mixed_model given that we also include random effects for market_value and capital, as shown below. Columns market_value and capital are the sums \(\hat{\beta}_1 + \hat{b}_{1,j}\) and \(\hat{\beta}_2 + \hat{b}_{2,j}\), respectively. Column (Intercept) is the sum \(\hat{\beta}_0 + \hat{b}_{0,j}\).

coef(full_mixed_model)$firm

A data.frame: 11 × 3

	(Intercept)	market_value	capital
	<dbl>	<dbl>	<dbl>
General Motors	-15.9552583	0.08936163	0.3746270
US Steel	-37.3981285	0.16343240	0.4206200
General Electric	3.7069150	0.02144198	0.1453769
Chrysler	-16.9962883	0.09295769	0.3041952
Atlantic Refining	6.5953958	0.01146421	0.1027958
IBM	-14.2108882	0.08333600	0.2855949
Union Oil	0.9675705	0.03090458	0.1371497
Westinghouse	-2.7054789	0.04359251	0.1826596
Goodyear	3.9889246	0.02046783	0.1116272
Diamond Match	-3.5486176	0.04650499	0.1985645
American Steel	-10.2172843	0.06954077	0.2331584

Exercise 17

We can see that these estimated intercepts in model_varying_intercept and mixed_intercept_model are very similar. Therefore, what are the advantages of a Mixed-Effects model over a model with fixed-effects only?

2.3. Estimation

The previous section skipped the estimation phase. However, we have to point out that maximum likelihood estimation (MLE) is still present in Mixed-Effects modelling. Nevertheless, MLE is performed in a different way. Recall that OLS only has a single variance component \(\sigma^2\), but in Mixed-Effects modelling, we have the variance component from each random effect.

Having said that, Mixed-Effects modelling performs what we call restricted MLE (R-MLE). Overall, R-MLE starts out with obtaining the estimate \(\hat{\sigma}^2\) via OLS (and, therefore, the regression estimates \(\hat{\beta}_0, \hat{\beta}_1, \dots, \hat{\beta}_k\) in the presence of \(k\) regressors which are the fixed effects). Then, we follow a second MLE with the primary \(n\) residuals obtained from OLS in specific linear combinations. This will allow for estimating the remaining variance components of the random effects.

2.4. Prediction

We can make two classes of predictions with Mixed-Effects models:

1. To predict on an existing group, we find that group’s regression coefficients (and therefore model function) by summing the fixed effects and (if present) the random effects, then use that model function to make predictions.

2. To predict on a new group (using a mean prediction), we use the fixed effects as the regression coefficients (because the random effects have mean zero) and use that model function to make predictions.

For predictions on an existing group in our training set we have:

round(predict(full_mixed_model, newdata = tibble(
  firm = "General Motors",
  market_value = 2000, capital = 1000
)), 2)

1: 537.4

If we wanted to predict the investment for General Motors with a market_value of USD \(\$2,000\) million and capital of USD \(\$1,000\) million, then our answer would be USD \(\$537.4\) million. This prediction uses \(\hat{\beta}_0\), \(\hat{\beta}_1\), \(\hat{\beta}_2\), \(\hat{b}_{0, j}\), \(\hat{b}_{1, j}\), and \(\hat{b}_{2, j}\).

Whereas that for predictions on American companies in general, we have:

round(predict(full_mixed_model,
  newdata = tibble(
    firm = "New Company",
    market_value = 2000, capital = 1000
  ),
  allow.new.levels = TRUE
), 2)

1: 341.51

If we wanted to predict the MEAN investment for American companies with a market_value of USD \(\$2,000\) million and capital of USD \(\$1,000\) million, then our answer would be USD \(\$341.51\) million. This prediction only uses \(\hat{\beta}_0\), \(\hat{\beta}_1\), and \(\hat{\beta}_2\).

3. Wrapping Up on Mixed-Effects Modelling

• In many different cases, when there is a correlation structure in our observations, OLS models are not suitable for our inferential or predictive inquiries.

• Therefore, linear Mixed-Effects models are suitable for correlated observations. Nonetheless, the model’s complexity will also be in function of our specific inquiries.

• We can even extend the Mixed-Effects approach to generalized linear models (GLMs)!