Lecture 6 - Local Regression

Today’s Learning Goals

By the end of this lecture, you should be able to:

• Define the concept of local regression.

• Model and perform piecewise constant, linear, and continuous linear local regressions.

• Extend the concept of \(k\)-NN classification to a regression framework.

• Define and apply locally weighted scatterplot smoother regression.

Loading Libraries

options(repr.matrix.max.rows = 10)
source("../scripts/support_functions.R")
library(tidyverse)
library(broom)
library(modelr)
library(caret)
library(gridExtra)

It is time to put aside regression techniques on the global conditioned mean and check local alternatives suitable for predictions.

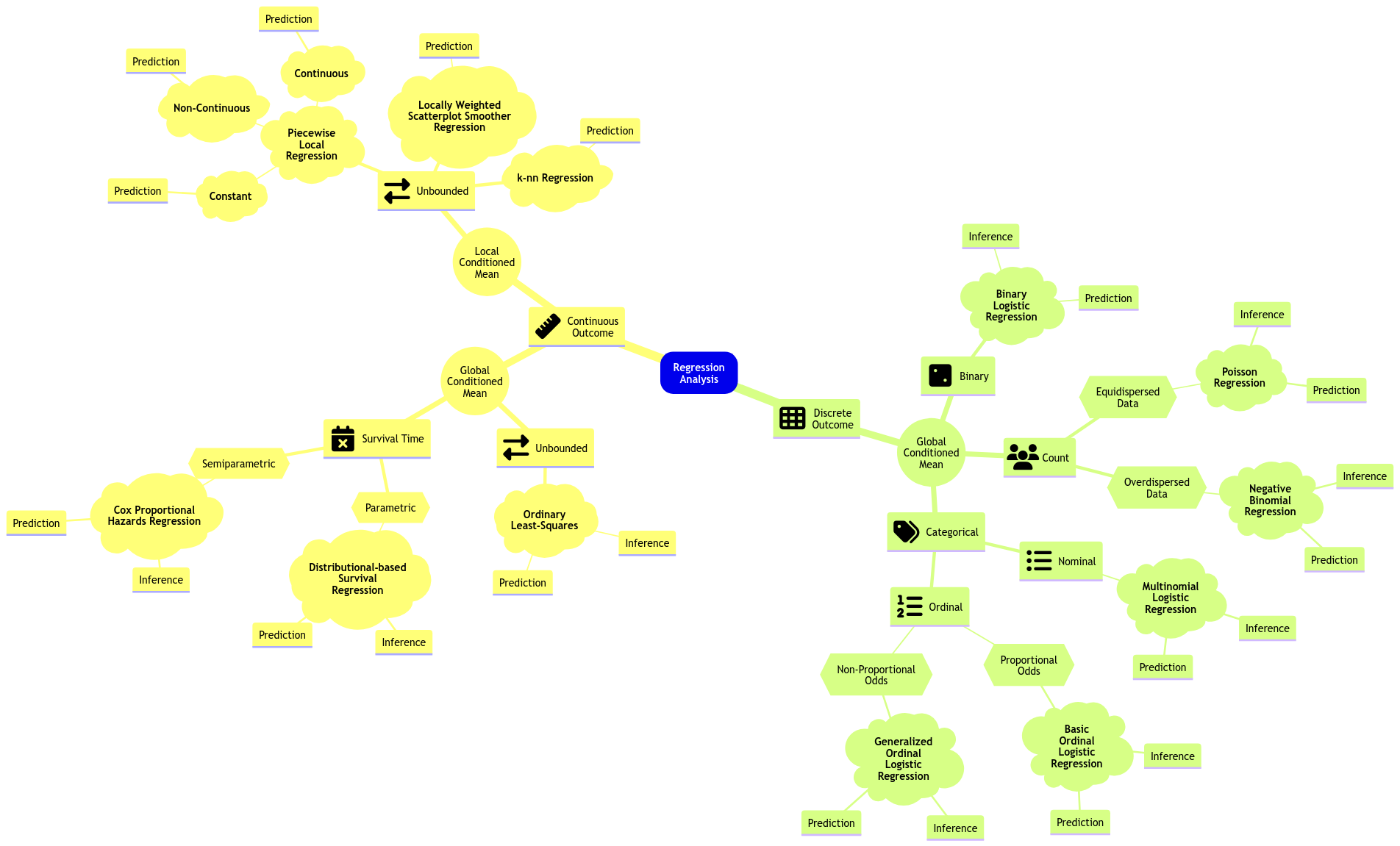
Fig. 15 Expanded regression modelling mind map (click on the image to zoom in).

1. Piecewise Local Regression

Retaking our initial motivation in this course, the classical linear regression model (Ordinary Least-squares, OLS) is focused on the conditional mean on the regressors:

\[ \mathbb{E}(Y_i \mid X_{i,j} = x_{i,j}) = \beta_0 + \beta_1 x_{i,1} + \ldots + \beta_k x_{i,k} \; \; \; \; \text{since} \; \; \; \; \mathbb{E}(\varepsilon_i) = 0. \]

We already stated that a model of this class, i.e. parametric, favours interpretability when we aim to make inference on the response and regressors.

Nonetheless, suppose our goal is an accurate prediction in many complex frameworks (e.g., non-linear). In that case, the global linearity in models such as the OLS case is not that flexible.

Therefore, we can use local regression techniques.

1.1. Piecewise Constant Regression

This regression technique is based on fitting different local OLS regressions. The step function is the key concept here.

Important

The idea behind the step function is to break the range of the regressor into intervals. In each interval, we adjust a constant. We obtain the average response in that interval.

Let us take the 2-\(d\) framework. For the \(i\)th observation in the sample, suppose we have a respose \(Y_i\) subject to a regressor \(X_i\).

Instead of making a global parametric assumption, we break the range of the regressor into \(q\) knots \(c_1, c_2, \dots, c_q\). Hence, the regressor will be sectioned in bins changing from continuous to categorical. The step functions are merely dummy variables.

\[\begin{split}\begin{equation*} C_0(X_i) = I(X_i < c_1) = \begin{cases} 1 \; \; \; \; \mbox{if $X_i < c_1$},\\ 0 \; \; \; \; \mbox{otherwise.} \end{cases} \end{equation*}\end{split}\]

\[\begin{split}\begin{equation*} C_1(X_i) = I(c_1 \leq X_i < c_2) = \begin{cases} 1 \; \; \; \; \mbox{if $c_1 \leq X_i < c_2$},\\ 0 \; \; \; \; \mbox{otherwise.} \end{cases} \end{equation*}\end{split}\]

\[\vdots\]

\[\begin{split}\begin{equation*} C_{q - 1}(X_i) = I(c_{q-1} \leq X_i < c_q) = \begin{cases} 1 \; \; \; \; \mbox{if $c_{q-1} \leq X_i < c_q$},\\ 0 \; \; \; \; \mbox{otherwise.} \end{cases} \end{equation*}\end{split}\]

\[\begin{split}\begin{equation*} C_q(X_i) = I(c_q \leq X_i) = \begin{cases} 1 \; \; \; \; \mbox{if $c_q \leq X_i$},\\ 0 \; \; \; \; \mbox{otherwise.} \end{cases} \end{equation*}\end{split}\]

Then, we run an OLS model based on these previous step functions and not the continuous \(X_i\).

The regression model becomes

\[ Y_i = \beta_0 + \beta_1 C_1(X_i) + \beta_2 C_2(X_i) + \dots + \beta_{q-1} C_{q-1}(X_i) + \beta_q C_q(X_i) + \varepsilon_i. \]

Attention

The step function \(C_0(X_i)\) does not appear in the model given that \(\beta_0\) can be interpreted as the response’s mean when \(X_i < c_1\) (i.e., the rest of the \(q\) step functions are equal to zero).

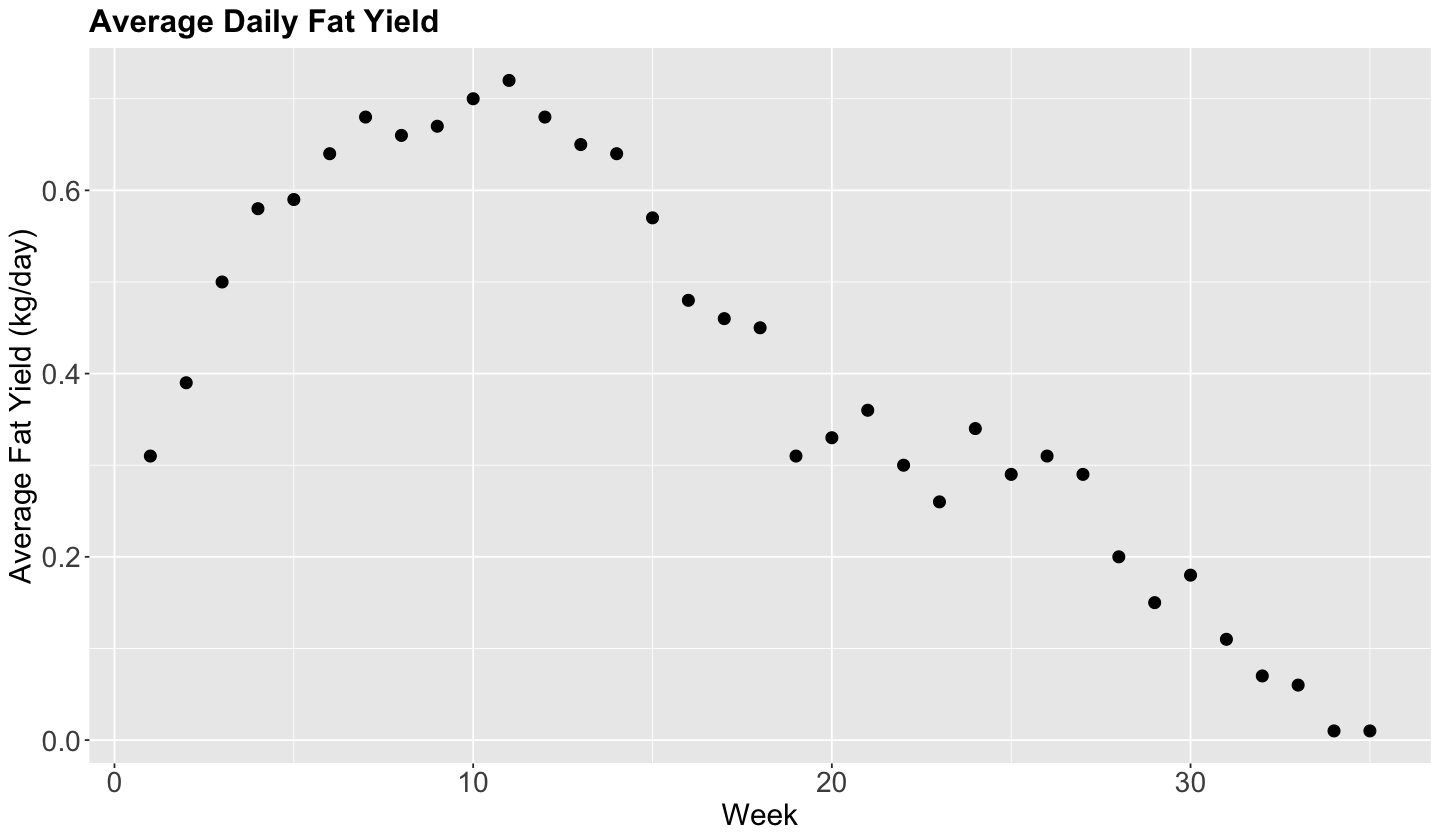
Cow Milk Dataset

We will use the dataset provided by Henderson and McCulloch (1990). The whole dataset contains the average daily milk fat yields from a cow in kg/day, from week 1 to 35.

fat_content <- suppressMessages(read_csv("../datasets/milk_fat.csv"))
str(fat_content)

spc_tbl_ [35 × 2] (S3: spec_tbl_df/tbl_df/tbl/data.frame)
 $ week: num [1:35] 1 2 3 4 5 6 7 8 9 10 ...
 $ fat : num [1:35] 0.31 0.39 0.5 0.58 0.59 0.64 0.68 0.66 0.67 0.7 ...
 - attr(*, "spec")=
  .. cols(
  ..   week = col_double(),
  ..   fat = col_double()
  .. )
 - attr(*, "problems")=<externalptr> 

options(repr.plot.height = 9, repr.plot.width = 20)

plot_cow <- fat_content %>% 
  ggplot(aes(week, fat)) +
  geom_point(size = 3) +
  labs(x = "Week", y = "Average Fat Yield (kg/day)") +
  ggtitle("Average Daily Fat Yield") +
  theme(
    plot.title = element_text(size = 31, face = "bold"),
    axis.text = element_text(size = 21),
    axis.title = element_text(size = 27))        
plot_cow

Let us fit a piecewise constant regression with \(q = 4\) knots.

# Define the number of step functions (q + 1)
breaks_q <- 5

# Create the steps for week.
fat_content <- fat_content %>% mutate(steps = cut(fat_content$week, breaks = breaks_q, 
  right = FALSE))
# Checking levels in steps
levels(fat_content$steps)

# Showing the new column steps.
head(fat_content)
tail(fat_content)

1. '[0.966,7.8)'
2. '[7.8,14.6)'
3. '[14.6,21.4)'
4. '[21.4,28.2)'
5. '[28.2,35)'

A tibble: 6 × 3

week	fat	steps
<dbl>	<dbl>	<fct>
1	0.31	[0.966,7.8)
2	0.39	[0.966,7.8)
3	0.50	[0.966,7.8)
4	0.58	[0.966,7.8)
5	0.59	[0.966,7.8)
6	0.64	[0.966,7.8)

A tibble: 6 × 3

week	fat	steps
<dbl>	<dbl>	<fct>
30	0.18	[28.2,35)
31	0.11	[28.2,35)
32	0.07	[28.2,35)
33	0.06	[28.2,35)
34	0.01	[28.2,35)
35	0.01	[28.2,35)

We can now fit the model_steps with formula = fat ~ steps via lm().

Attention

Note that estimate is the difference between each category with respect to the baseline [0.966,7.8).

model_steps <- lm(fat ~ steps, data = fat_content)
tidy(model_steps) %>% mutate_if(is.numeric, round, 3)
glance(model_steps) %>% mutate_if(is.numeric, round, 3)

A tibble: 5 × 5

term	estimate	std.error	statistic	p.value
<chr>	<dbl>	<dbl>	<dbl>	<dbl>
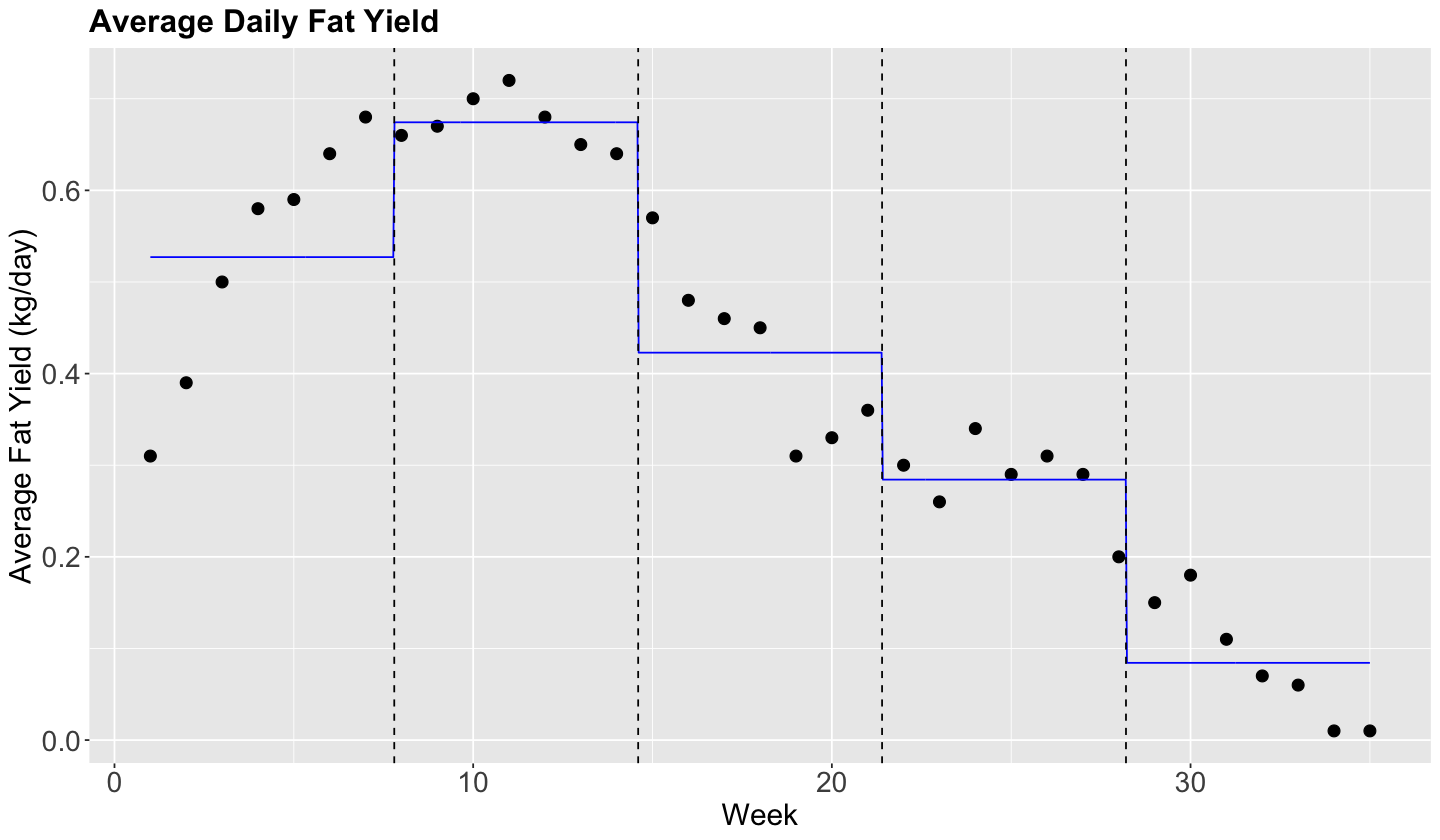
(Intercept)	0.527	0.031	16.897	0.000
steps[7.8,14.6)	0.147	0.044	3.335	0.002
steps[14.6,21.4)	-0.104	0.044	-2.364	0.025
steps[21.4,28.2)	-0.243	0.044	-5.504	0.000
steps[28.2,35)	-0.443	0.044	-10.037	0.000

A tibble: 1 × 12

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual	nobs
<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
0.875	0.859	0.083	52.648	0	4	40.34	-68.68	-59.348	0.204	30	35

# Creating the grid for predictions.
grid <- fat_content %>%
  data_grid(week = seq_range(week, 1000)) %>%
  mutate(steps = cut(week, breaks_q, right = FALSE)) %>%
  add_predictions(model_steps)

# Creating labels and plotting values for the knots.
labs <- levels(fat_content$steps)
steps <- tibble(
  lower = as.numeric(sub("\\[(.+),.*", "\\1", labs)),
  upper = as.numeric(sub("[^,]*,([^]]*)\\)", "\\1", labs))
)

# Plotting.
plot_cow +
  geom_line(aes(week, pred), data = grid, color = "blue") +
  geom_vline(xintercept = steps$lower[-1], linetype = "dashed")

grid

A tibble: 1000 × 3

week	steps	pred
<dbl>	<fct>	<dbl>
1.000000	[0.966,7.8)	0.5271429
1.034034	[0.966,7.8)	0.5271429
1.068068	[0.966,7.8)	0.5271429
1.102102	[0.966,7.8)	0.5271429
1.136136	[0.966,7.8)	0.5271429
⋮	⋮	⋮
34.86386	[28.2,35)	0.08428571
34.89790	[28.2,35)	0.08428571
34.93193	[28.2,35)	0.08428571
34.96597	[28.2,35)	0.08428571
35.00000	[28.2,35)	0.08428571

Exercise 23

Discuss the importance of this class of a local regression strategy of having breakpoints by regressor when having prediction inquiries.

1.2. Non-Continuous Piecewise Linear Regression

Note in the previous plot, though, that the functions should not be constant inside an interval. Instead, there is an approximately linear behaviour in each interval.

Can we capture that? Yes we can!

All we need to do, is to add \(\color{green}{\text{interaction terms}}\) between the step functions \(C_j(X_i)\), for \(j = 1, \dots, q\), with \(X_i\):

\[\begin{equation*} Y_i = \beta_0 + \color{red}{\beta_1 C_1(X_i) + \dots + \beta_q C_q(X_i)} + \beta_{q + 1} X_i + \color{green}{\beta_{q + 2} X_i C_1(X_i) + \dots + \beta_{2q + 1} X_i C_q(X_i)} + \varepsilon_i. \end{equation*}\]

Let us see what happens in this model:

• If \(X_i < c_1\), then our model is: \(Y_i = \beta_0 + \beta_{q + 1}X_i\)

• If \(c_1 \leq X_i < c_2\), then our model is: \(Y_i = \beta_0 + \color{red}{\beta_1} + (\beta_{q + 1} + \color{green}{\beta_{q + 2}}) X_i\)

• If \(c_2 \leq X_i < c_3\), then our model is: \(Y_i = \beta_0 + \color{red}{\beta_2} + (\beta_{q + 1} + \color{green}{\beta_{q + 3}}) X_i\)

\[\vdots\]

• If \(c_{q-1} \leq X_i < c_q\), then our model is: \(Y_i = \beta_0 + \color{red}{\beta_{q -1}} + (\beta_{q + 1} + \color{green}{\beta_{2q}}) X_i\)

• If \(c_q \leq X_i\), then our model is: \(Y_i = \beta_0 + \color{red}{\beta_q} + (\beta_{q + 1} + \color{green}{\beta_{2q + 1}}) X_i\)

So, for each interval, we have an \(\color{red}{\text{additional intercept}}\) and an \(\color{green}{\text{additional slope}}\).

Now, we will check if the model fitting looks better in fat_content. Note that the right hand side in the formula, within lm(), is merely a model with interaction week * steps.

# We need to add the interaction between steps and week.
model_piecewise_linear <- lm(fat ~ week * steps, data = fat_content)

## Let us create our grid for predictions,
grid <- fat_content %>%
  data_grid(week = seq_range(week, 1000)) %>%
  mutate(steps = cut(week, breaks_q, right = FALSE)) %>%
  add_predictions(model_piecewise_linear)

## Plotting
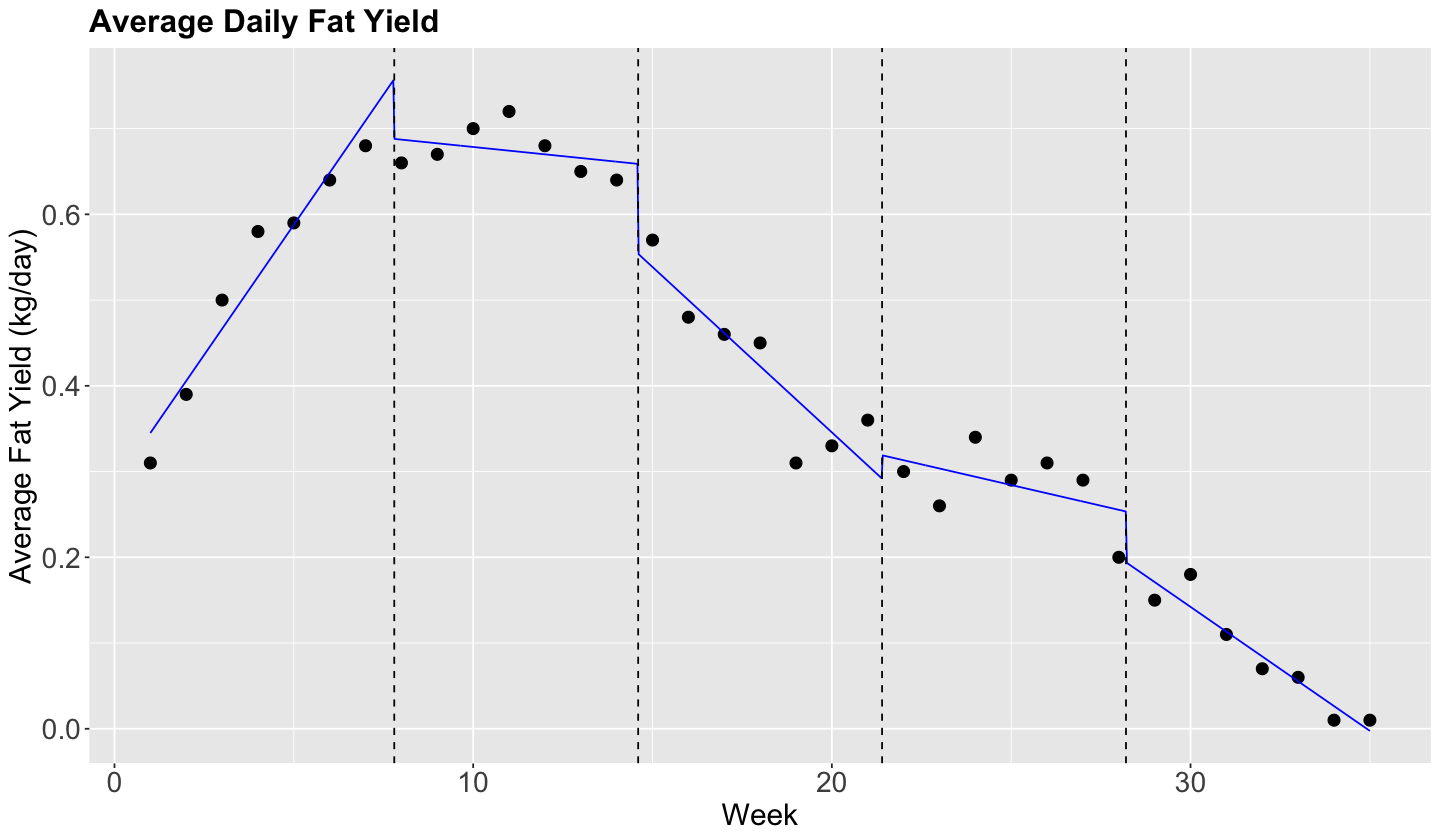
plot_cow +
  geom_line(aes(week, pred), data = grid, color = "blue") +
  geom_vline(xintercept = steps$lower[-1], alpha = 1, linetype = "dashed")

Let us check the model’s summary.

tidy(model_piecewise_linear) %>% mutate_if(is.numeric, round, 3)
glance(model_piecewise_linear) %>% mutate_if(is.numeric, round, 3)

A tibble: 10 × 5

term	estimate	std.error	statistic	p.value
<chr>	<dbl>	<dbl>	<dbl>	<dbl>
(Intercept)	0.284	0.031	9.261	0.000
week	0.061	0.007	8.846	0.000
steps[7.8,14.6)	0.437	0.083	5.289	0.000
steps[14.6,21.4)	0.833	0.128	6.505	0.000
steps[21.4,28.2)	0.241	0.175	1.379	0.180
steps[28.2,35)	0.726	0.222	3.266	0.003
week:steps[7.8,14.6)	-0.065	0.010	-6.696	0.000
week:steps[14.6,21.4)	-0.099	0.010	-10.228	0.000
week:steps[21.4,28.2)	-0.070	0.010	-7.248	0.000
week:steps[28.2,35)	-0.090	0.010	-9.235	0.000

A tibble: 1 × 12

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual	nobs
<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
0.98	0.973	0.036	135.294	0	9	72.264	-122.528	-105.419	0.033	25	35

However, the local regression lines are disconnected. Can we fix that?

1.3. Continuous Piecewise Linear Regression

We can impose restrictions to make sure that the lines are connected to each other. Therefore, we need to introduce the concept of the hinge function.

For the \(i\)th observation, this model can be defined as follows:

\[Y_i = \beta_0 + \beta_1 X_i +\beta_2 (X_i - c_1)_{+} + \dots + \beta_{q+1} (X_i - c_q)_{+} + \varepsilon_i,\]

where the hinge function for the knot \(c_j\)

\[\begin{split} (X_i - c_j)_{+} = \begin{cases} 0 \; \; \; \; \mbox{if $X_i < c_j$},\\ X_i - c_j \; \; \; \; \mbox{if $X_i \geq c_j$}. \end{cases} \end{split}\]

We do not need to fit separate OLS linear regressions but one. In the lm() function, within formula on the right-hand side along with the standalone regressor X, we have to add up the following term I((X - c_j)*(X >= c_j)) by knot c_j.

We need to obtain the corresponding knots in fat_content (\(q = 4\)):

levels(fat_content$steps)
knots <- c(7.8, 14.6, 21.4, 28.2)

1. '[0.966,7.8)'
2. '[7.8,14.6)'
3. '[14.6,21.4)'
4. '[21.4,28.2)'
5. '[28.2,35)'

Now, let us fit this model.

model_piecewise_cont_linear <- lm(fat ~ week + I((week - knots[1]) * (week >= knots[1])) +
  I((week - knots[2]) * (week >= knots[2])) +
  I((week - knots[3]) * (week >= knots[3]))+
  I((week - knots[4]) * (week >= knots[4])),
data = fat_content
)

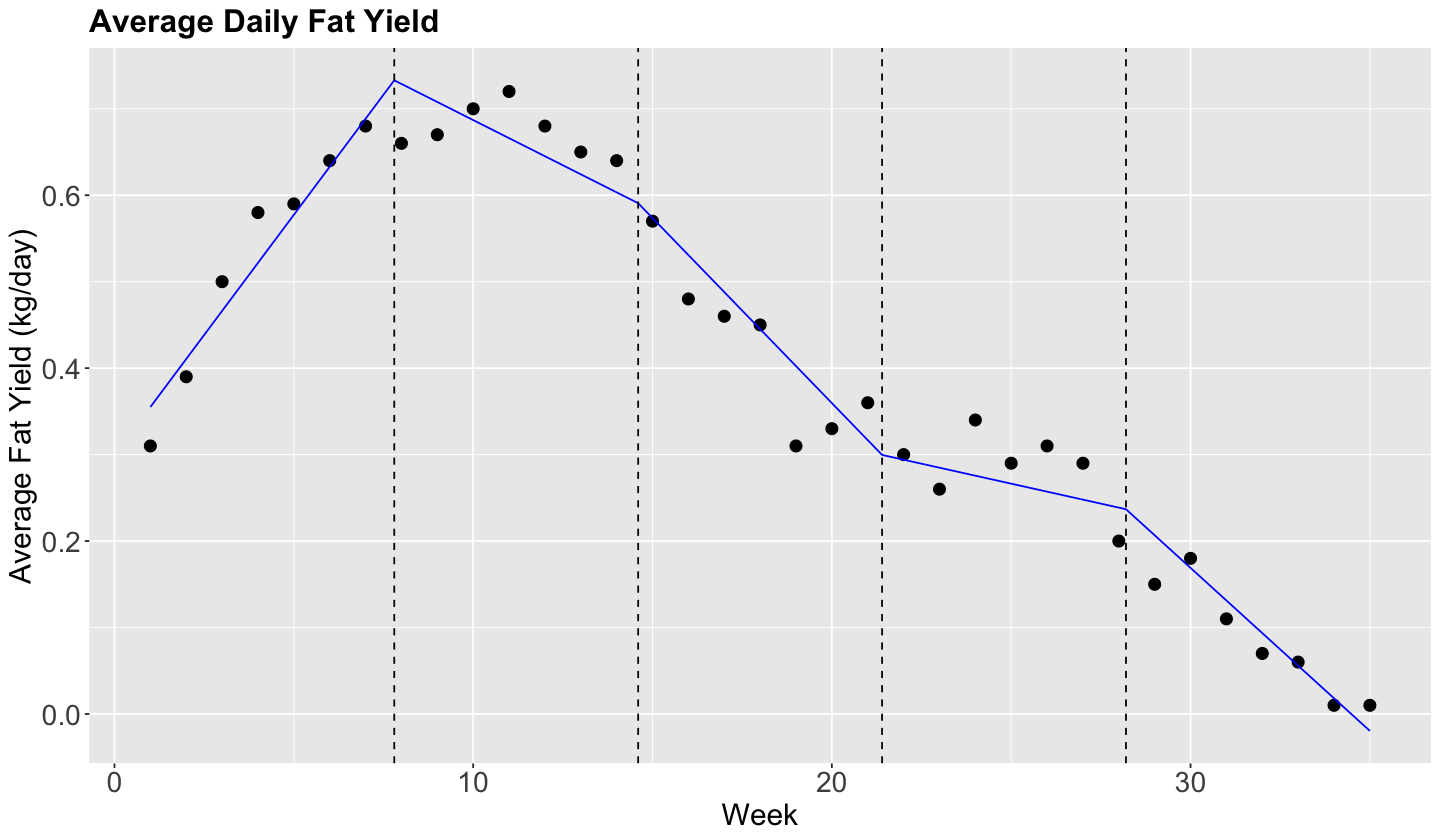
Now, we will check if the model fitting looks better in fat_content.

# Let us create our grid for predictions,
grid <- fat_content %>%
  data_grid(week = seq_range(week, 1000)) %>%
  mutate(steps = cut(week, breaks_q, right = FALSE)) %>%
  add_predictions(model_piecewise_cont_linear)

# Plotting
plot_cow +
  geom_line(aes(week, pred), data = grid, color = "blue") +
  geom_vline(xintercept = steps$lower[-1], alpha = 1, linetype = "dashed")

Let us check the model’s summary.

tidy(model_piecewise_cont_linear) %>% mutate_if(is.numeric, round, 3)
glance(model_piecewise_cont_linear) %>% mutate_if(is.numeric, round, 3)

A tibble: 6 × 5

term	estimate	std.error	statistic	p.value
<chr>	<dbl>	<dbl>	<dbl>	<dbl>
(Intercept)	0.299	0.032	9.453	0.000
week	0.056	0.006	9.604	0.000
I((week - knots[1]) * (week >= knots[1]))	-0.076	0.010	-7.854	0.000
I((week - knots[2]) * (week >= knots[2]))	-0.022	0.009	-2.414	0.022
I((week - knots[3]) * (week >= knots[3]))	0.034	0.009	3.700	0.001
I((week - knots[4]) * (week >= knots[4]))	-0.028	0.010	-2.924	0.007

A tibble: 1 × 12

r.squared	adj.r.squared	sigma	statistic	p.value	df	logLik	AIC	BIC	deviance	df.residual	nobs
<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>	<dbl>
0.969	0.963	0.042	180.119	0	5	64.587	-115.175	-104.287	0.051	29	35

2. \(k\)-NN Regression

Attention

I have been using the letter \(k\) to denote the number of regressors in any general regression model. Nevertheless, this letter is reserved for groups of \(k\) observations in this framework. Therefore, I will switch to the letter \(p\) to denote the number of regressors in this framework.

The idea behind \(k\)-NN regression is finding the \(k\) observations in our training dataset of size \(n\) (with \(p\) features \(x_j\) per observation) closest to the new point we want to predict.

Next, we calculate the average \(\bar{y}^{(k)}\) of the responses of those \(k\) observations. That is our new prediction.

How do we obtain those \(k\) observations? Based on the values of the respective \(p\) features, we determine which \(k\) observations (out from the \(n\) in the training set) have the smallest distance metric (e.g., Euclidean distance \(D^{(\text{Training, New})}\)) to the features of the new point.

\[ D^{(\text{Training, New})} = \sqrt{\sum_{j = 1}^p \Big( x_j^{\text{(Training)}} - x_j^{\text{(New)}} \Big)^2} \]

Important

We would compute \(n\) distances \(D^{(\text{Training, New})}\) using the same “New” observation. Then, there will be \(k\) “Training” observations to be chosen out of these \(n\) distances (where \(n\) represents the total number of training data points).

Things to keep in mind:

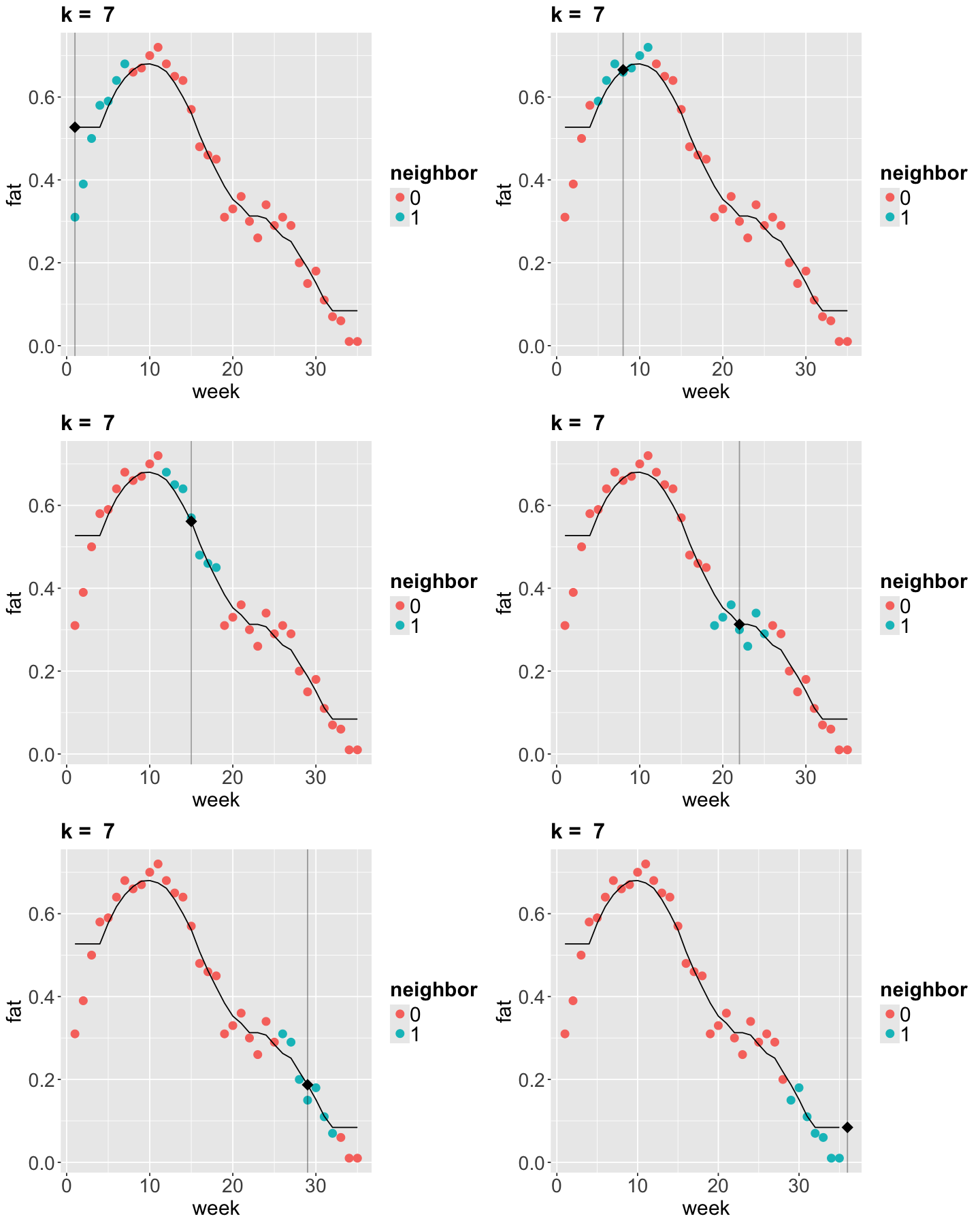
1. If \(k = 1\), there will be no training error. Nevertheless, we might (and probably will) overfit badly.

2. As we increase \(k\), more “smooth” the regression will be. At some point, we will start underfitting.

Exercise 24

What are the consequences of overfitting a training set in further test sets?

A. There are no consequences at all; predictions will be highly accurate in any further test set.

B. The trained model will be so oversimplified that we will have a high bias in further test set predictions.

C. The trained model will be so overfitted that it will also explain random noise in training data. Therefore, we cannot generalize this model in further test set predictions.

Now let us run \(k\)-NN algorithm on the fat_content dataset.

options(repr.plot.height = 20, repr.plot.width = 18)

k <- 7 # Use odd numbers here so there is no missmatch on how the ties are handled.

## Running k-NN regression
my_knn <- knnreg(fat ~ week, data = fat_content, k = k)
grid <- fat_content %>%
  data_grid(week) %>%
  add_predictions(my_knn)

## Generating the plots.
p <- list()
for (i in 1:6) {
  p[[i]] <- knn_plot((i - 1) * 7 + 1, k) + geom_line(aes(week, pred), data = grid)
}

grid.arrange(grobs = p, ncol = 2)

3. Locally Weighted Scatterplot Smoother (LOWESS) Regression

Suppose we want to predict the response \(y\) for a given \(x\). For example, we want to predict the fat content of cow milk in week 10. The idea of LOWESS is:

1. Find the closest points to week 10 (how many points is a parameter that we define).

2. From the selected points, we assign weights based on these distances. The closest the point is, the more weight it will receive (weights are determined as in weighted least-squares by default in loess()).

3. Next, for the \(i\)th point in the span, using weighted least-squares for a second degree polynomial for instance, we minimize the sum of squared errors considering the weight \(w_i\) as follows:

\[ \sum_i w_i \left(y_i - \beta_0-\beta_1 x_i-\beta_2 x_i^2\right)^2 \]

Important

Roughly speaking, weighted least-squares allow us to assume a different variance \(\sigma_{x_i}^2\) for the \(i\)th observation (i.e., it can be shown mathematically that \(w_i = 1 / \sigma_{x_i}^2\)). This model will enable us to deal with heteroscedasticity.

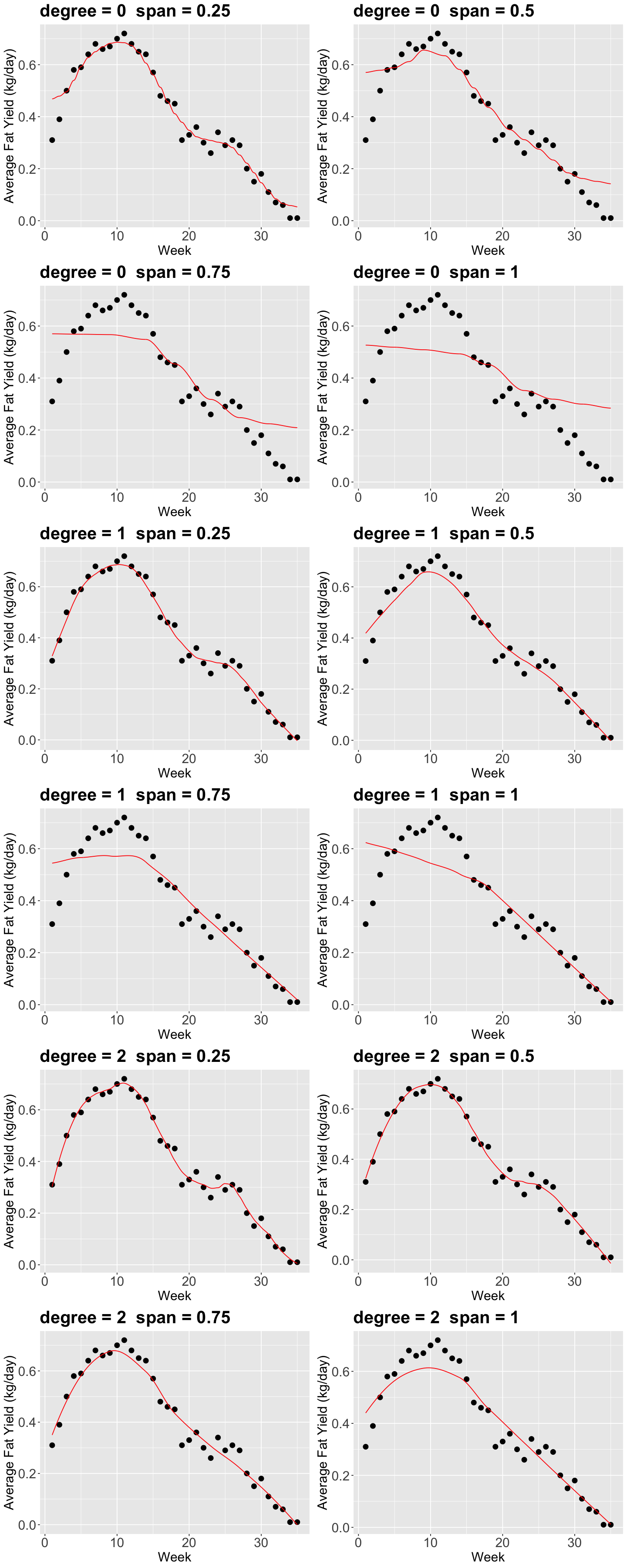
Now, there are a couple of things to consider in loess():

• The parameter span (between 0 and 1) defines the “size” of your neighbourhood. To be more exact, it specifies the proportion of points considered as neighbours of \(x\). The higher the proportion, the smoother the fitted surface will be.

• The parameter degree, specifies if you are fitting a constant (degree= 0), a linear model (degree = 1), or a quadratic model (degree = 2). By quadratic, we mean \(\beta_0+\beta_1 x_i+\beta_2 x_i^2\).

p <- list()
i <- 1
for (degree in seq(0, 2, 1)) {
  for (span in seq(0.25, 1, 0.25)) {
    
    suppressWarnings(model_loess <- loess(fat ~ week, span = span, degree = degree, data = fat_content))

    # We create our grid for predictions.
    grid <- fat_content %>%
      data_grid(week = seq_range(week, 1000)) %>%
      add_predictions(model_loess)

    # Plotting.
    p[[i]] <- plot_cow +
      geom_line(aes(week, pred), data = grid, color = "red") +
      theme(
        plot.title = element_text(size = 24),
        axis.text = element_text(size = 18),
        axis.title = element_text(size = 18)
      ) +
      ggtitle(paste0("degree = ", degree, "  span = ", span))

    i <- i + 1
  }
}

grid.arrange(grobs = p, ncol = 2)

4. Wrapping Up

• Local regression is a great tool for addressing predictive inquiries.

• Nonetheless, we will lose our inferential interpretability.

• The key concept in local regression techniques is “how local we want our model to be.”