Lecture 8 - Missing Data#
Today’s Learning Goals#
By the end of this lecture, you should be able to:
Identify and explain the three common types of missing data mechanisms.
Identify a potential consequence of removing missing data on downstream analyses.
Identify a potential consequence of a mean imputation method on downstream analyses.
Identify the four steps involved with a multiple imputation method for handling missing data.
Use the
micepackage inRto fit multiple imputed models.
Loading Libraries#
options(repr.matrix.max.rows = 20)
library(tidyverse)
library(nycflights13)
library(mice)
1. Types of Missing Data#
In Statistics, there are three types of missing data:
Missing completely at random (MCAR).
Missing at random (MAR).
Missing not at random (MNAR).
It is in our best interest to identify the type of missing data we have. Proper identification will determine the class of approach we will take to deal with missingness in any statistical analysis.
1.1. Missing Completely At Random (MCAR)#
In this type, missing data appear totally by chance. Hence, missingness is independent of the data. Roughly speaking, all our observations (rows in the dataset) have the same chance of containing missing data (i.e., an NA in one of the columns).
Important
It is the ideal class of missing data since there is no missingness pattern.
Example
We are trying to count the number of car accidents in Vancouver. To do that, we are monitoring the traffic in 100 strategic points of the city with cameras. Say that we count how many vehicles passed by each one of those cameras for every minute of the day. We have 101 variables: time, Camera_1, …, Camera_100.
Suppose that any camera has a \(1\%\) chance of failing for any given minute. If a camera fails, you get MCAR data for that minute.
1.2. Missing At Random (MAR)#
In this type, missingness depends on the observed data we have. Therefore, we could use some imputation techniques for this missingness, such as multiple imputation (to be covered later on today), based on the rest of our available data (a hot deck imputation technique).
Important
Missing data imputation techniques are divided into two classes:
Hot deck: Those incomplete rows in our current dataset are imputed using the information provided by the complete rows within the same dataset.
Cold deck: Those incomplete rows in our current dataset are imputed using the information provided by the complete rows of another dataset with the same column structure.
The scope of this lecture pertains to hot deck techniques.
Example
Following up with the previous example, an external device is attached to the cameras to increase the image quality at low light situations (night time) and we have the recording time in our dataset. The external device is activated from 6 p.m. to 5 a.m. However, the device has a \(10\%\) chance of not working in a given minute. The chances are not the same for all the observations but depend on the data we observed, more specifically, night time.
1.3. Missing Not At Random (MNAR)#
This is the most serious type of missingness since the MNAR data depends on unobservable quantities.
Example
With the previous example, if we did not record time, we would be MNAR data since we do not have any other information rather than just the car count. Another missingness cause of this type would be that, as the cameras get older, their probability of failure increases, but we cannot check this from our observed data.
2. Handling Missing Data#
We will explore different techniques to impute missing data based on the type of missingness.
2.1. Listwise Deletion#
It is the simplest way to deal with missing data.
Is there any missing data in your row? If yes, we just remove the row.
If the data is MCAR, we are not introducing bias by removing the rows. We can still get unbiased estimators for whichever our analysis is, such as regression coefficients.
We can also estimate the standard errors correctly, but they will be higher than they could be since we discard incomplete observations.
Exercise 27
Are these higher standard errors related to the MCAR nature of the deleted rows?
A. Yes.
B. No.
Let us start with our lecture’s toy dataset: the flights dataset from the package nycflights13. It contains the on-time data of 336,776 flights that departed New York City in 2013.
We will use the following columns:
dep_delay: departure delays in minutes.arr_delay: arrival delays in minutes.carrier: two-letter carrier abbreviation.
We will try getting the mean dep_delay per carrier, but we have missing data in dep_delay, which will return a summary with NAs.
flights |>
group_by(carrier) |>
summarise(dep_delay = mean(dep_delay)) |>
mutate_if(is.numeric, round, 3)
| carrier | dep_delay |
|---|---|
| <chr> | <dbl> |
| 9E | NA |
| AA | NA |
| AS | NA |
| B6 | NA |
| DL | NA |
| EV | NA |
| F9 | NA |
| FL | NA |
| HA | 4.901 |
| MQ | NA |
| OO | NA |
| UA | NA |
| US | NA |
| VX | NA |
| WN | NA |
| YV | NA |
Assuming data is MCAR, if we want to make a listwise deletion to get the means by carrier, we just use na.rm = TRUE in mean().
flights |>
group_by(carrier) |>
summarise(dep_delay = mean(dep_delay, na.rm = TRUE)) |>
mutate_if(is.numeric, round, 2)
| carrier | dep_delay |
|---|---|
| <chr> | <dbl> |
| 9E | 16.73 |
| AA | 8.59 |
| AS | 5.80 |
| B6 | 13.02 |
| DL | 9.26 |
| EV | 19.96 |
| F9 | 20.22 |
| FL | 18.73 |
| HA | 4.90 |
| MQ | 10.55 |
| OO | 12.59 |
| UA | 12.11 |
| US | 3.78 |
| VX | 12.87 |
| WN | 17.71 |
| YV | 19.00 |
Nonetheless, we have to be careful. If the missing data in flights is not MCAR, we can introduce serious bias in our estimates (means in this case) for some given statistical approach.
But, why a bias?
Let us set another example to explain the bias issue when data missingness is present. Suppose that people with low income have a higher chance of omitting their income (as a numeric variable) in a given survey used for Regression Analysis. Then, if we just drop those rows, we are skewing our analysis towards people with higher income without knowing. So, there will be a bias in our regression estimates.
Exercise 28
Let us retake the previous survey example regarding low-income respondents. Suppose this survey collects additional information, such as the respondent’s specific neighbourhood, which is a complete column. Then, you could match this extra information with some other neighbourhood databases identifying low, middle, and high-income areas.
What class of missing data are these missing numeric incomes in the survey?
A. MCAR.
B. MAR.
C. MNAR.
2.2. Mean Imputation#
The title is very suggestive. Let us just use the mean of our variable of interest to impute the missing data.
Caution
This imputation technique can only be used with continuous and count-type variables!
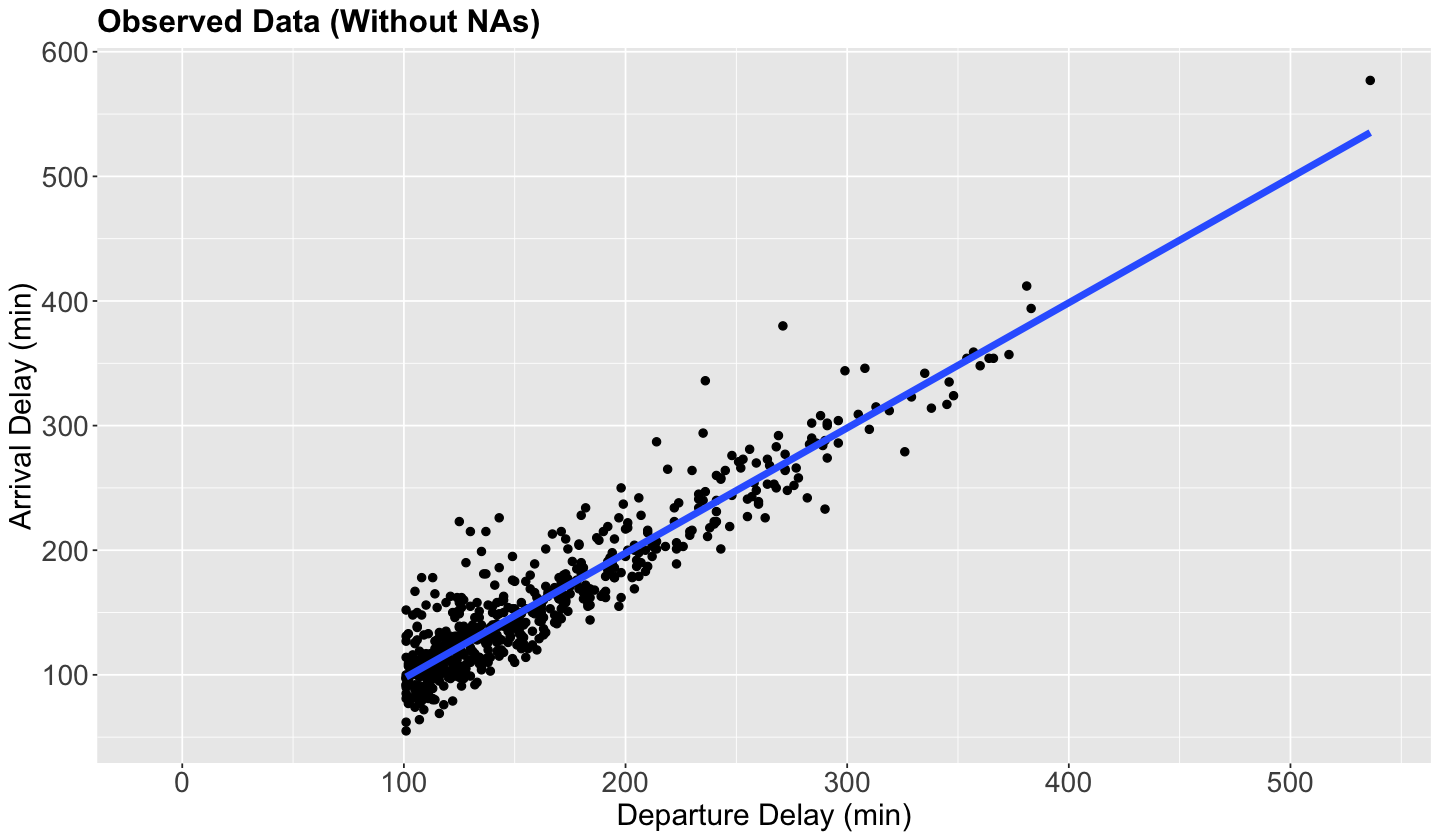
Re-taking the flights dataset, for the exercise’s sake (not to be generalized to other data cases), we will filter those observations with NAs in arr_delay OR dep_delay values larger than 100 minutes. Then, we will only sample 1000 flights.
options(repr.plot.height = 7, repr.plot.width = 12)
set.seed(123)
sampled_flights <- flights |>
select(dep_delay, arr_delay) |>
filter(is.na(arr_delay) | dep_delay > 100) |>
sample_n(size = 1000)
scatterplot_flights <- sampled_flights |>
ggplot(aes(dep_delay, arr_delay)) +
geom_point(size = 2) +
ggtitle("Observed Data (Without NAs)") +
geom_smooth(method = "lm", formula = y ~ x, se = FALSE, linewidth = 2) +
theme(
plot.title = element_text(size = 19, face = "bold"),
axis.text = element_text(size = 17),
axis.title = element_text(size = 18)
) +
scale_x_continuous(breaks = seq(0, 500, 100)) +
xlab("Departure Delay (min)") +
ylab("Arrival Delay (min)")
Attention
Note the condition dep_delay > 100 is also depicted in the plot.
The blue line is just the estimated Ordinary Least-squares (OLS) linear regression of dep_delay versus arr_delay with 593 complete observations. Nonetheless, since the conditional is is.na(arr_delay) | dep_delay > 100 (i.e., OR), we would eventually have an imputed subset of observations with negative dep_delay, i.e., flights on time but missing arr_delay. We can see some rows under this situation in the below data frame.
This missigness pattern will provide a particular behaviour in our subsequent mean imputations.
sampled_flights |> filter(is.na(arr_delay) & !is.na(dep_delay))
| dep_delay | arr_delay |
|---|---|
| <dbl> | <dbl> |
| 2 | NA |
| 1 | NA |
| 43 | NA |
| -4 | NA |
| 8 | NA |
| 7 | NA |
| 31 | NA |
| -11 | NA |
| 12 | NA |
| -2 | NA |
| ⋮ | ⋮ |
| 59 | NA |
| -6 | NA |
| 79 | NA |
| 105 | NA |
| -5 | NA |
| 36 | NA |
| 41 | NA |
| -3 | NA |
| -6 | NA |
| 120 | NA |
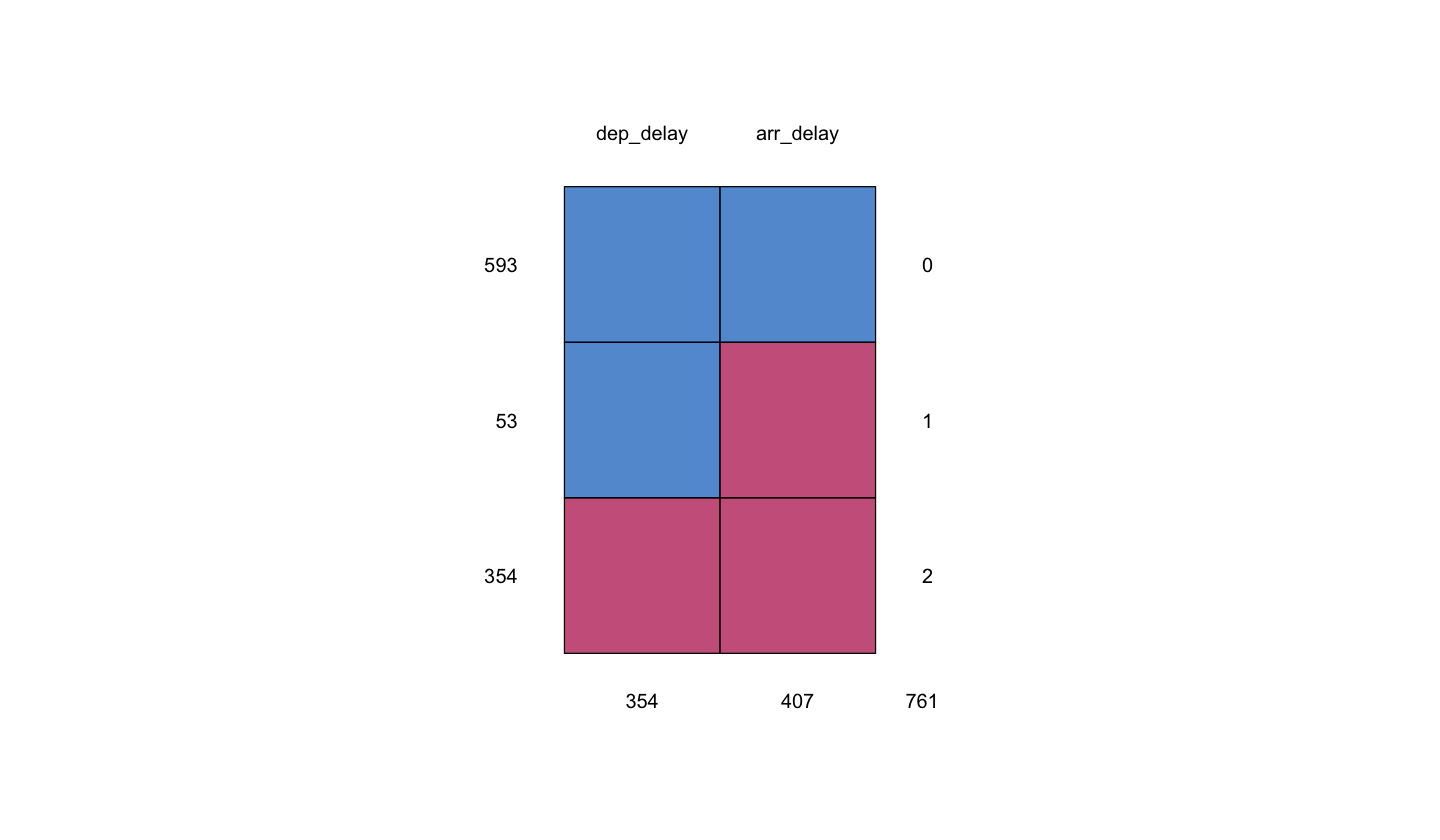
Moving along, it is necessary to perform an exploratory data analysis (EDA) on our data missingness. We can use the function md.pattern() from the package mice to display missing data patterns.
md.pattern(sampled_flights)
We can interpret the \(4 \times 3\) matrix (and diagram) above in the following way:
Important
For the \(4 \times 3\) table, in the columns
dep_delayandarr_delay(rows 1 to 3):0indicates that neither of the variables is missing.1indicates that one variable is present.2indicates that two variables are missing.Row numbers indicate those observations with the variables present/missing:
593indicates the number of rows wheredep_delayandarr_delayare jointly present.53indicates the number of rows wheredep_delayis present andarr_delayis missing.354indicates the number of rows wheredep_delayandarr_delayare jointly missing.Then, we have \(593 + 53 + 354 = 1000\) rows in total (our sample size!).
Column numbers indicate those observations with the standalone missing variables:
354indicates the number of rows wheredep_delayis missing, regardless of whetherarr_delayis missing or not.407indicates the number of rows wherearr_delayis missing, regardless of whetherdep_delayis missing or not.
For the columns in the diagram
dep_delayandarr_delay, the coloured cells indicate:Blue indicates that the variable is present.
Red indicates that the variable is missing.
Therefore, we have 593 observations with non-missing data in both dep_delay and arr_delay, 53 with arr_delay missing, and 354 with both dep_delay and arr_delay missing.
The md.pattern() summary shows that our sample does NOT contain observations where dep_delay is missing and arr_delay is present.
Now, we will impute the overall means of dep_delay and arr_delay.
# Manually imputing the missing data.
sampled_flights_imputed <- sampled_flights |>
mutate(flag = as_factor(if_else(is.na(dep_delay) | is.na(arr_delay), "missing", "observed"))) |>
mutate(dep_delay = if_else(is.na(dep_delay), mean(dep_delay, na.rm = TRUE), dep_delay)) |>
mutate(arr_delay = if_else(is.na(arr_delay), mean(arr_delay, na.rm = TRUE), arr_delay))
# Now, using mice() from the mice package.
sampled_flights_imputed_mice <- mice(sampled_flights, m = 1, method = "mean", maxit = 1)
iter imp variable
1 1 dep_delay arr_delay
head(sampled_flights) # Checking first rows in our original sample.
| dep_delay | arr_delay |
|---|---|
| <dbl> | <dbl> |
| NA | NA |
| 178 | 185 |
| 109 | 107 |
| 2 | NA |
| NA | NA |
| 198 | 182 |
head(sampled_flights_imputed_mice$where) # Checking logical flags for missing data in mice() object.
| dep_delay | arr_delay | |
|---|---|---|
| 1 | TRUE | TRUE |
| 2 | FALSE | FALSE |
| 3 | FALSE | FALSE |
| 4 | FALSE | TRUE |
| 5 | TRUE | TRUE |
| 6 | FALSE | FALSE |
flag <- pmin(rowSums(sampled_flights_imputed_mice$where), 1) # Flag for imputed data.
flag <- if_else(flag == 0, "observed", "missing") # Flag for imputed data.
sampled_flights_imputed_mice <- mice::complete(sampled_flights_imputed_mice) |> mutate(flag = flag)
# Sanity check of amount of imputed values.
table(sampled_flights_imputed$flag)
missing observed
407 593
table(sampled_flights_imputed_mice$flag)
missing observed
407 593
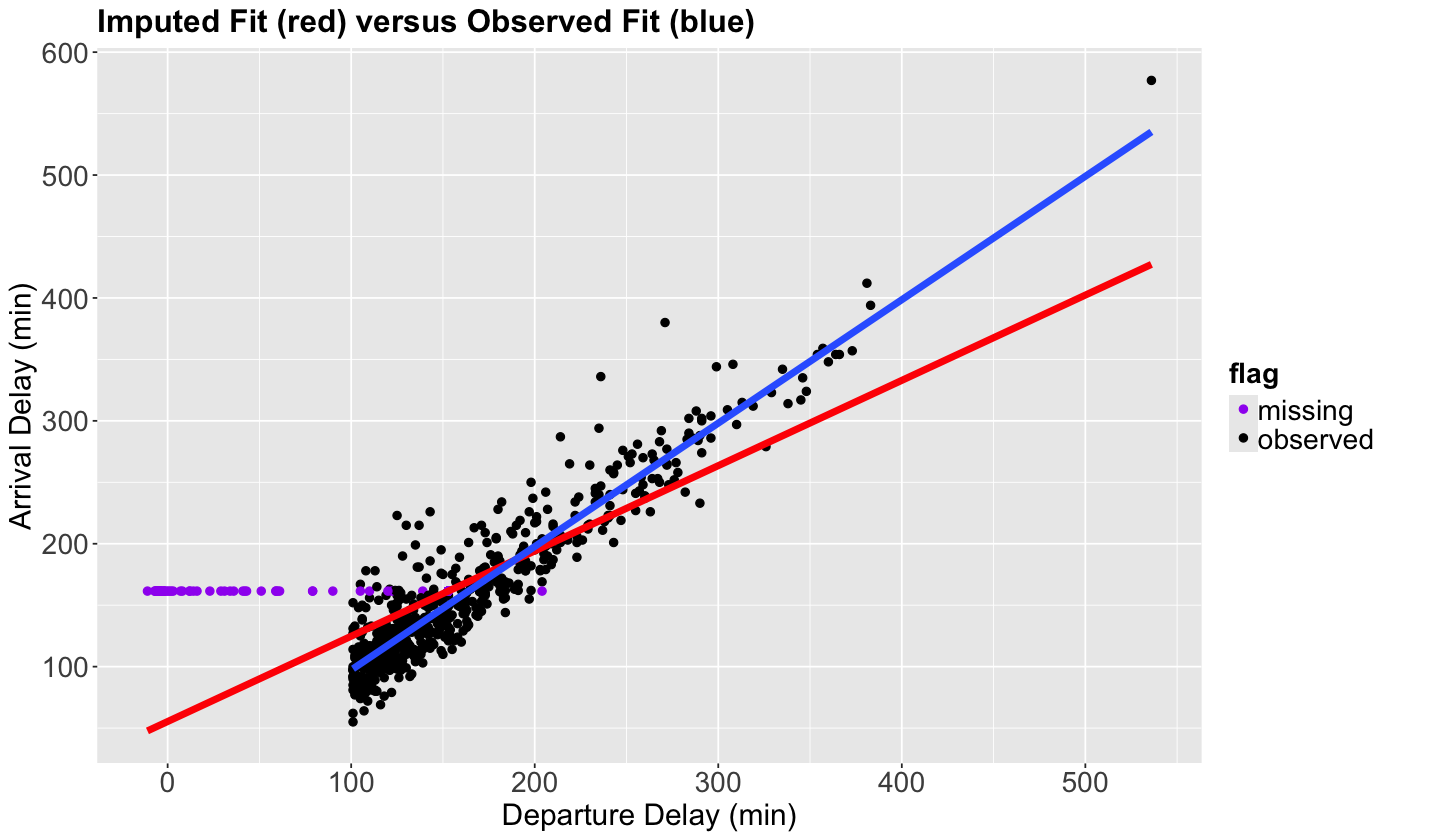
We will now plot the imputed values as purple points, and another estimated OLS linear regression in red with the \(n = 1000\) sampled observations (non-imputed AND imputed).
Note the horizontal pattern in the imputed purple points, which is the subset of observations with the particular behaviour we previously mentioned.
## Plotting imputed versus observed.
scatterplot_flights <- sampled_flights_imputed_mice |>
ggplot() +
geom_point(aes(dep_delay, arr_delay, color = flag), size = 2) +
geom_smooth(aes(dep_delay, arr_delay), linewidth = 2, formula = y ~ x, color = "red", method ='lm', se = FALSE) +
geom_smooth(aes(dep_delay, arr_delay), linewidth = 2, formula = y ~ x, method = "lm", data = sampled_flights, se = FALSE) +
scale_color_manual(values = c("purple", "black")) +
ggtitle("Imputed Fit (red) versus Observed Fit (blue)") +
theme(
plot.title = element_text(size = 19, face = "bold"),
axis.text = element_text(size = 17),
axis.title = element_text(size = 18),
legend.text = element_text(size = 17, margin = margin(r = 1, unit = "cm")),
legend.title = element_text(size = 17, face = "bold")
) +
scale_x_continuous(breaks = seq(0, 500, 100)) +
xlab("Departure Delay (min)") +
ylab("Arrival Delay (min)")
Also, notice that by imputing the mean, we are artificially reducing the standard deviation of our data which is a drawback of mean imputation.
# Standard deviation of the complete observed data.
sampled_flights |>
na.omit() |>
summarise_all(.funs = sd) |>
mutate_if(is.numeric, round, 2)
| dep_delay | arr_delay |
|---|---|
| <dbl> | <dbl> |
| 61.05 | 65.45 |
# Standard deviation of all the data (imputed and non-imputed).
sampled_flights_imputed |>
select(-flag) |>
summarise_all(.funs = sd) |>
mutate_if(is.numeric, round, 2)
| dep_delay | arr_delay |
|---|---|
| <dbl> | <dbl> |
| 56.54 | 50.38 |
Important
This behaviour on the sample standard deviation is explained given its mathematical computation:
Note that this \(s\) will be quite sensitive when imputing values with the corresponding mean \(\bar{x}\).
Having said all this, let us proceed to a more “robust” imputation method.
2.3. Regression Imputation#
From the black points (complete observations) in the previous plot, we can notice a clear positive relation between arr_delay changes with dep_delay. Hence, why not using the estimated OLS linear regression in blue (fitted with those complete 593 observations) to estimate those missing values?
We can do it automatically via mice() using method = "norm.predict".
sampled_flights_imputed_reg <- mice(sampled_flights, method = "norm.predict", seed = 1, m = 1, print = FALSE)
flag <- pmin(rowSums(sampled_flights_imputed_reg$where), 1) # Flag for imputed data.
flag <- if_else(flag == 0, "observed", "missing") # Flag for imputed data.
sampled_flights_imputed_reg <- complete(sampled_flights_imputed_reg) |>
mutate(flag = flag)
# Sanity check of amount of imputed values.
table(sampled_flights_imputed_reg$flag)
missing observed
407 593
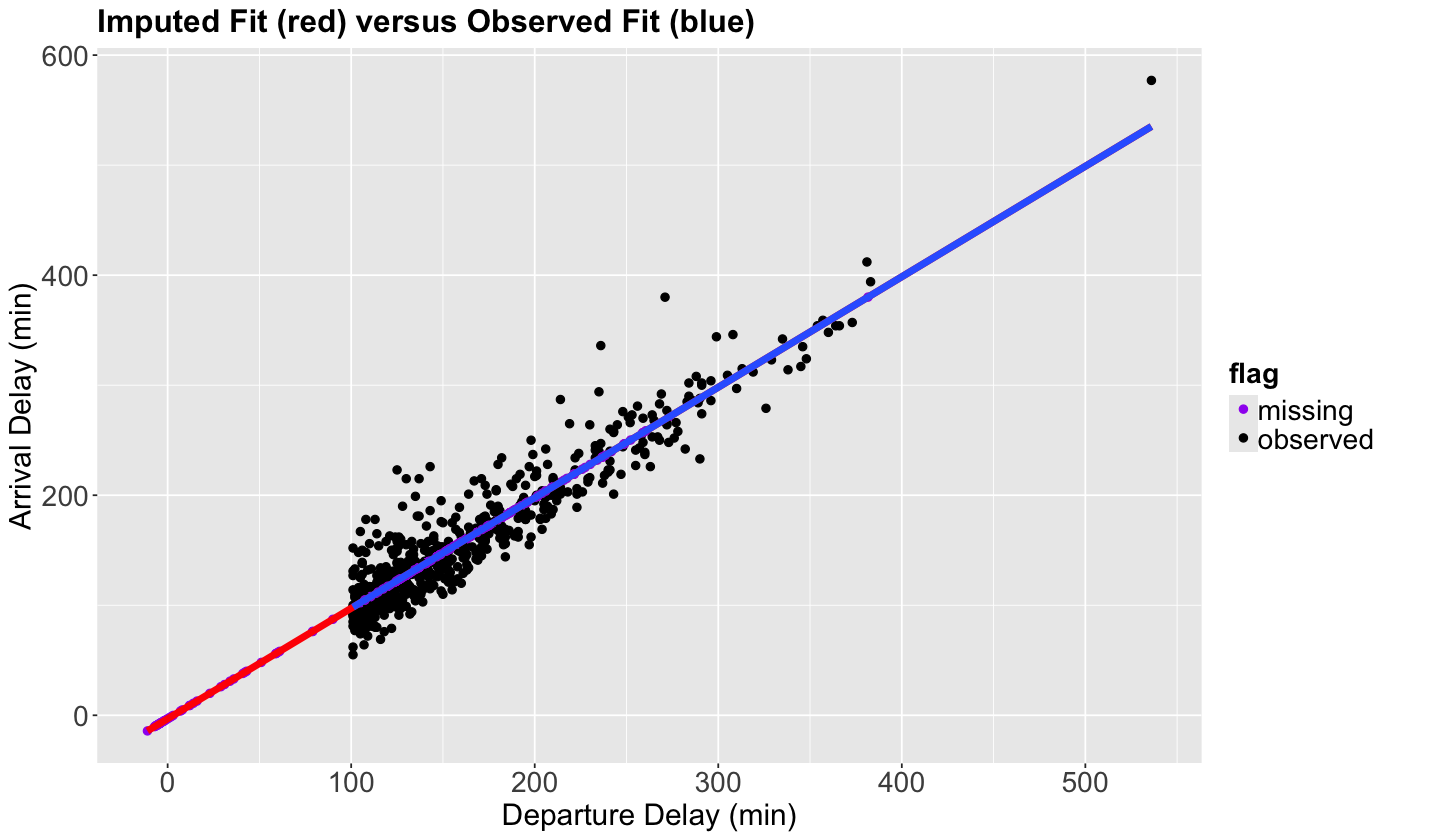
Then, we plot our dataset (including those imputted data points using OLS).
## Plotting imputed versus observed.
scatterplot_flights_reg <- sampled_flights_imputed_reg |>
ggplot() +
geom_point(aes(dep_delay, arr_delay, color = flag), size = 2) +
geom_smooth(aes(dep_delay, arr_delay), linewidth = 2, formula = y ~ x, color = "red", method='lm', se = FALSE) +
geom_smooth(aes(dep_delay, arr_delay), linewidth = 2, formula = y ~ x, method = "lm", data = sampled_flights, se = FALSE) +
scale_color_manual(values = c("purple", "black")) +
ggtitle("Imputed Fit (red) versus Observed Fit (blue)") +
theme(
plot.title = element_text(size = 19, face = "bold"),
axis.text = element_text(size = 17),
axis.title = element_text(size = 18),
legend.text = element_text(size = 17, margin = margin(r = 1, unit = "cm")),
legend.title = element_text(size = 17, face = "bold")
) +
scale_x_continuous(breaks = seq(0, 500, 100)) +
xlab("Departure Delay (min)") +
ylab("Arrival Delay (min)")
Now, all the purple points (imputed values) are on the imputed fit (red) line, which is now just an extension of the observed fit (blue) line.
Since the method imputes all the points perfectly in the regression line, we will reinforce the data’s relationships. For example, let us calculate the correlation of the imputed data vs the observed data.
# Only complete observations.
as_tibble(cor(sampled_flights, use = "complete.obs")) |>
mutate_if(is.numeric, round, 2)
| dep_delay | arr_delay |
|---|---|
| <dbl> | <dbl> |
| 1.00 | 0.94 |
| 0.94 | 1.00 |
# All observations (complete and imputed).
as_tibble(cor(sampled_flights_imputed_reg |> select(-flag))) |>
mutate_if(is.numeric, round, 2)
| dep_delay | arr_delay |
|---|---|
| <dbl> | <dbl> |
| 1.00 | 0.96 |
| 0.96 | 1.00 |
Attention
Regression imputation seems to have a more “inline” behaviour for imputed data than just using the mean since we are basically using regression-fitted values for this missing data. Moreover, we can extend this framework to more than two variables simultaneously.
Nevertheless, we still fix our imputation on a single set of estimated regression parameters. In fact, we could have a more clever strategy that would rely on different simulated datasets given what prior COMPLETE information we have in our dataset.
2.4. Last Observation Carried Over#
Another method that we might see out there is imputing data by repeating the previous observation. This is more frequent when dealing with temporal data, and will be out of the scope of this course.
2.5. Multiple Imputation#
Having explored mean and regression imputations, let us proceed to a simulation-based method called multiple imputation.
We have seen that using a single value for the imputation causes problems, such as reducing our dataset variance. Then, a handy approach is the multiple imputation method.
The idea here is, instead of imputing one value for missing data, we impute multiple values. But how can we do it?
We can do it via the mice() function, which offers this multiple imputation method. MICE stands for Multiple Imputation by Chained Equations.
Roughly speaking, for a data frame data, the four automatic steps in this R function are the following:
Create
mcopies of this dataset:data_1,data_2,…,data_m.In each copy, impute the missing data with different values (the observed values will remain the same).
Carry out the analysis for each dataset separately. For example, fit an OLS linear regression model for each one of the datasets
data_1,data_2,…,data_mwhen you have a continuous variable to impute.Combine the separate models into one final pooled model.
We would use our pooled model, fitted with our response of interest subject to our regressor set, to answer our inferential or predictive inquiries. The below diagram provides a clearer perspective
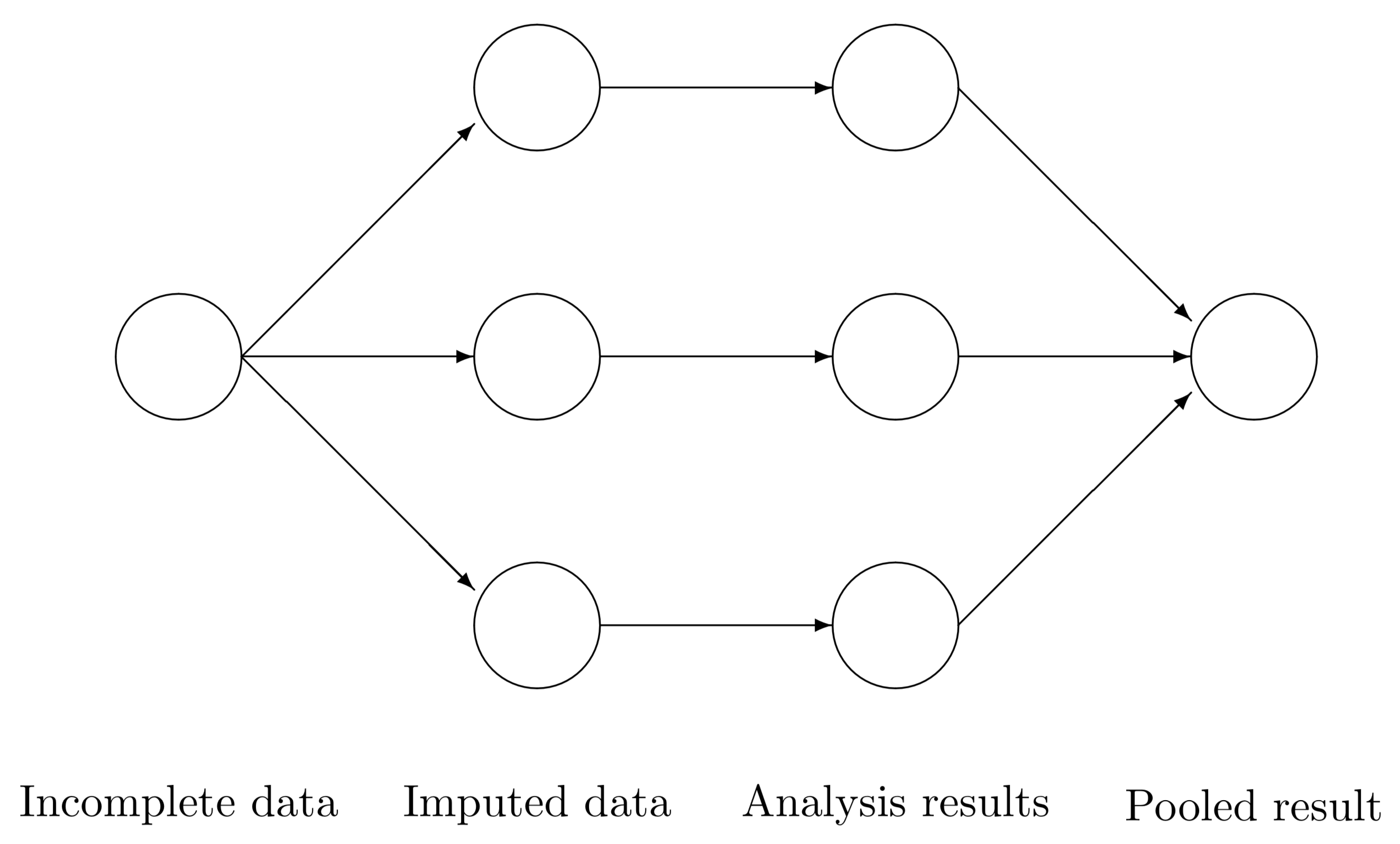
Fig. 18 Source: van Buuren (2012).#
Important
Note that the suitable regression model will be chosen accordingly depending on the nature of our variable of interest to impute. Therefore, mice() will use the following regression models:
Binary Logistic regression for binary variables.
Multinomial Logistic regression for categorical and nominal variables.
Ordinal Logistic regression for categorical and ordinal variables.
We have to make sure to set up the correct variable type before imputing!
Now, how do we impute the missing data in step 2?
By default, mice() implements the predictive mean matching (PMM) found in Rubin (1987) on page 166.
This is a univariate Bayesian method that does the following for each column:
Estimate the OLS linear regression coefficient \(\hat{\beta}_1\) and \(\hat{\sigma}\) of the column where the missing values to impute are located (as the response) versus the other column (as the regressor), using the observed complete rows only.
Draw \(\hat{\beta}_1^*\) and \(\hat{\sigma}^*\) using a proper posterior distribution.
Compute the fitted values for the column used as response in step (1), either using \(\hat{\beta}_1\) and \(\hat{\sigma}\) for those non-missing cases (i.e., \(\hat{y}_i\)) or \(\hat{\beta}_1^*\) and \(\hat{\sigma}^*\) (i.e., \(\hat{y}_i^*\)) for those missing cases.
For each fitted value \(\hat{y}_i^*\), we find a given number of donors (5 by default in
mice()) from all the \(\hat{y}_i\)s which are the closest ones to \(\hat{y}_i^*\).We randomly select one of these donors to impute the corresponding missing value.
The process is repeated
mtimes.
Important
Note that this algorithm also has a multivariate version in matrix notation.
Let us implement this univariate process with sampled_flights with m = 20.
set.seed(123) # We are running a simulation, this we need to set a seed.
sampled_flights_imputed_PMM <- mice(sampled_flights, m = 20, printFlag = FALSE)
sampled_flights_imputed_PMM
Class: mids
Number of multiple imputations: 20
Imputation methods:
dep_delay arr_delay
"pmm" "pmm"
PredictorMatrix:
dep_delay arr_delay
dep_delay 0 1
arr_delay 1 0
We can check the imputed values for a specific column (e.g., arr_delay) in these 20 datasets as follows:
sampled_flights_imputed_PMM$imp$arr_delay
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> | |
| 1 | 258 | 92 | 146 | 218 | 133 | 82 | 194 | 179 | 169 | 138 | 179 | 243 | 77 | 113 | 127 | 104 | 154 | 99 | 227 | 108 |
| 4 | 127 | 85 | 100 | 100 | 97 | 131 | 131 | 127 | 97 | 127 | 85 | 55 | 92 | 90 | 85 | 62 | 90 | 90 | 97 | 90 |
| 5 | 166 | 185 | 124 | 111 | 166 | 308 | 100 | 90 | 111 | 222 | 221 | 163 | 187 | 158 | 107 | 195 | 141 | 100 | 108 | 107 |
| 7 | 113 | 97 | 195 | 300 | 270 | 250 | 162 | 98 | 127 | 150 | 238 | 126 | 100 | 166 | 129 | 144 | 116 | 140 | 273 | 314 |
| 8 | 128 | 103 | 108 | 158 | 154 | 153 | 154 | 105 | 81 | 80 | 194 | 102 | 100 | 100 | 124 | 324 | 160 | 84 | 180 | 181 |
| 9 | 162 | 181 | 101 | 138 | 117 | 165 | 117 | 166 | 160 | 112 | 115 | 62 | 187 | 273 | 170 | 62 | 107 | 129 | 161 | 105 |
| 17 | 103 | 128 | 100 | 125 | 114 | 160 | 107 | 127 | 112 | 213 | 92 | 62 | 148 | 215 | 130 | 80 | 80 | 80 | 108 | 100 |
| 24 | 107 | 302 | 82 | 82 | 153 | 258 | 112 | 91 | 132 | 127 | 131 | 297 | 181 | 105 | 125 | 115 | 123 | 141 | 110 | 380 |
| 28 | 92 | 81 | 88 | 317 | 135 | 158 | 81 | 243 | 130 | 158 | 79 | 152 | 134 | 100 | 186 | 218 | 302 | 82 | 134 | 172 |
| 30 | 127 | 144 | 228 | 152 | 107 | 167 | 195 | 148 | 218 | 114 | 190 | 219 | 160 | 254 | 258 | 240 | 130 | 131 | 102 | 222 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| 975 | 138 | 114 | 312 | 148 | 132 | 137 | 140 | 160 | 162 | 112 | 109 | 209 | 117 | 285 | 113 | 119 | 179 | 92 | 201 | 292 |
| 977 | 100 | 106 | 274 | 223 | 119 | 137 | 104 | 112 | 114 | 105 | 130 | 242 | 98 | 160 | 119 | 110 | 152 | 77 | 143 | 129 |
| 979 | 253 | 176 | 124 | 161 | 178 | 317 | 190 | 158 | 186 | 178 | 116 | 116 | 140 | 131 | 142 | 140 | 87 | 308 | 201 | 115 |
| 982 | 158 | 162 | 127 | 153 | 143 | 137 | 215 | 250 | 81 | 137 | 244 | 201 | 160 | 116 | 91 | 175 | 201 | 130 | 183 | 180 |
| 985 | 160 | 315 | 216 | 161 | 114 | 132 | 97 | 90 | 124 | 136 | 234 | 189 | 120 | 92 | 271 | 139 | 204 | 150 | 221 | 98 |
| 986 | 62 | 85 | 97 | 62 | 97 | 92 | 62 | 98 | 97 | 97 | 90 | 92 | 98 | 97 | 98 | 62 | 92 | 90 | 90 | 100 |
| 991 | 158 | 104 | 170 | 108 | 126 | 109 | 152 | 118 | 300 | 149 | 218 | 69 | 148 | 149 | 85 | 153 | 160 | 139 | 89 | 250 |
| 992 | 100 | 135 | 128 | 103 | 98 | 158 | 122 | 124 | 111 | 109 | 124 | 122 | 120 | 103 | 128 | 158 | 158 | 114 | 128 | 158 |
| 993 | 131 | 201 | 115 | 114 | 133 | 100 | 160 | 137 | 152 | 112 | 96 | 257 | 184 | 167 | 120 | 131 | 135 | 323 | 138 | 130 |
| 994 | 174 | 138 | 158 | 81 | 124 | 132 | 110 | 97 | 131 | 108 | 110 | 128 | 166 | 94 | 98 | 135 | 157 | 208 | 103 | 271 |
Each row corresponds to a missing observation in your original dataset. The columns are the m imputed datasets that were created.
We can get each one of the m imputed datasets with complete().
# This is dataset number 3.
complete(sampled_flights_imputed_PMM, 3)
| dep_delay | arr_delay |
|---|---|
| <dbl> | <dbl> |
| 153 | 146 |
| 178 | 185 |
| 109 | 107 |
| 2 | 100 |
| 121 | 124 |
| 198 | 182 |
| 213 | 195 |
| 110 | 108 |
| 105 | 101 |
| 179 | 169 |
| ⋮ | ⋮ |
| 168 | 170 |
| 120 | 128 |
| 114 | 115 |
| 174 | 158 |
| 161 | 154 |
| 139 | 138 |
| 152 | 136 |
| 150 | 175 |
| 383 | 394 |
| 267 | 253 |
We can plot the imputed dataset number 3 a follows:
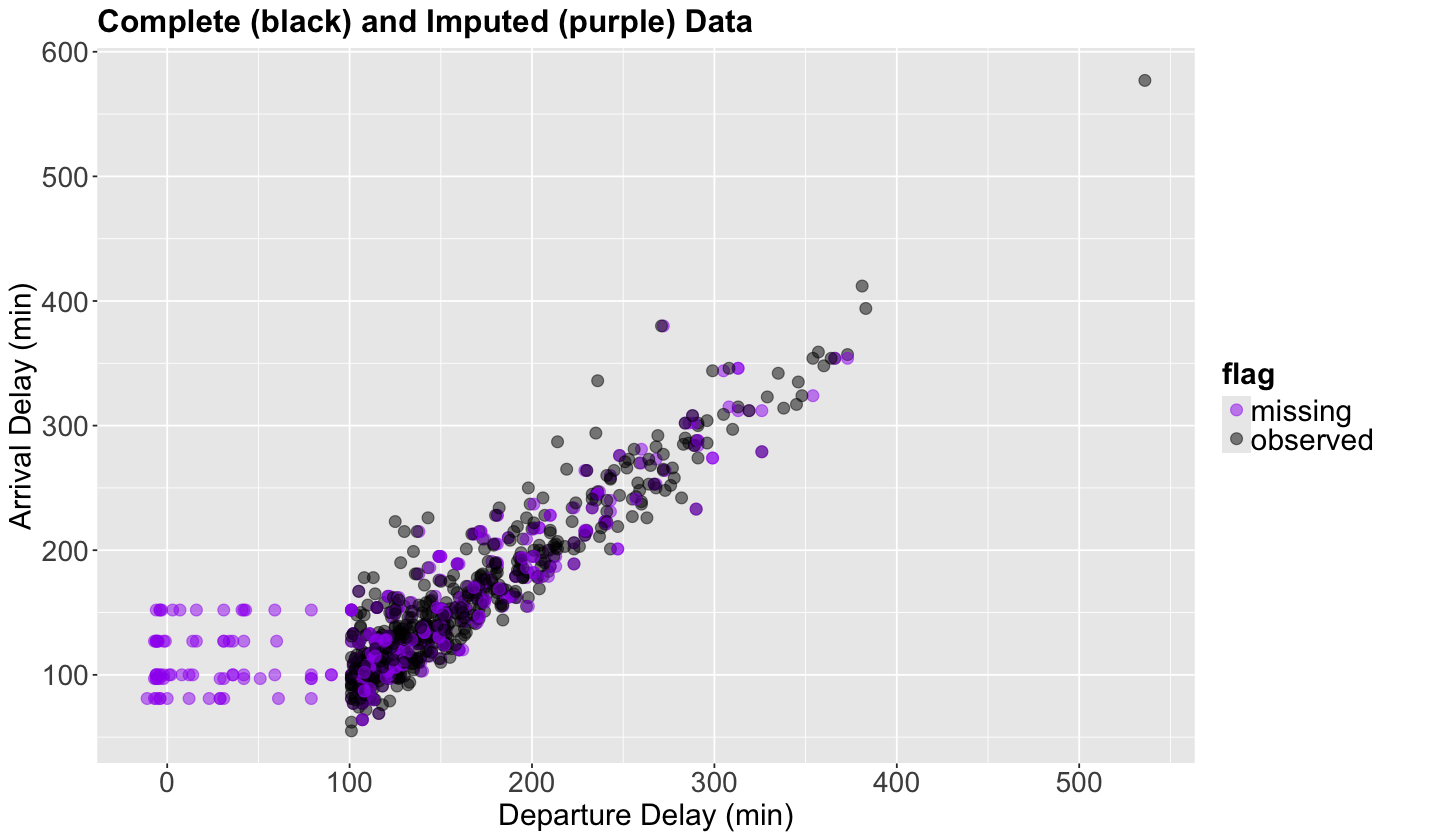
sampled_flights_imputed_PMM_3 <- cbind(complete(sampled_flights_imputed_PMM, 3), sampled_flights_imputed$flag)
sampled_flights_imputed_PMM_3_plot <- sampled_flights_imputed_PMM_3 |>
ggplot(aes(dep_delay, arr_delay)) +
geom_point(aes(colour = flag), size = 3, alpha = .5) +
scale_color_manual(values = c("purple", "black")) +
theme(
plot.title = element_text(size = 19, face = "bold"),
axis.text = element_text(size = 17),
axis.title = element_text(size = 18),
legend.text = element_text(size = 18, margin = margin(r = 1, unit = "cm")),
legend.title = element_text(size = 18, face = "bold")
) +
scale_x_continuous(breaks = seq(0, 500, 100)) +
xlab("Departure Delay (min)") +
ylab("Arrival Delay (min)") +
ggtitle("Complete (black) and Imputed (purple) Data")
Attention
Note this imputation method allows incomplete observations to be imputed with more realistic values, rather than just an overall mean or a fitted value coming from simple OLS regression (check purple points on top of the cloud of black points on the right-hand side). Nevertheless, it is not entirely perfect if it does not have enough complete information to impute (check purple points on the left-hand side where we do not have any complete data points in black).
Now, let us estimate an OLS linear regression for each one of the 20 imputed datasets in sampled_flights_imputed_PMM. Our response will be arr_delay subject dep_delay.
PMM_LR_models <- with(sampled_flights_imputed_PMM, lm(arr_delay ~ dep_delay))
print(PMM_LR_models)
call :
with.mids(data = sampled_flights_imputed_PMM, expr = lm(arr_delay ~
dep_delay))
call1 :
mice(data = sampled_flights, m = 20, printFlag = FALSE)
nmis :
dep_delay arr_delay
354 407
analyses :
[[1]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
30.6428 0.8202
[[2]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
21.8563 0.8677
[[3]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
35.0526 0.8003
[[4]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
29.967 0.821
[[5]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
26.5144 0.8451
[[6]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
27.2239 0.8385
[[7]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
29.7340 0.8223
[[8]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
28.0674 0.8332
[[9]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
28.6254 0.8354
[[10]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
27.6203 0.8414
[[11]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
25.4984 0.8484
[[12]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
31.2887 0.8183
[[13]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
22.0089 0.8653
[[14]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
25.2515 0.8534
[[15]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
29.8358 0.8192
[[16]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
24.0202 0.8576
[[17]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
22.100 0.868
[[18]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
33.2085 0.8029
[[19]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
30.6784 0.8208
[[20]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
36.0514 0.7932
We can access to each model separately as follows:
# Retrieving the third model.
PMM_LR_models$analyses[[3]]
Call:
lm(formula = arr_delay ~ dep_delay)
Coefficients:
(Intercept) dep_delay
35.0526 0.8003
Finally, let us combine the models altogether in a single pooled model.
pooled_PMM_LR_model <- pool(PMM_LR_models)
print(pooled_PMM_LR_model)
Class: mipo m = 20
term m estimate ubar b t dfcom
1 (Intercept) 20 28.262276 5.2134906153 1.668369e+01 22.731369026 998
2 dep_delay 20 0.833603 0.0001842278 5.009364e-04 0.000710211 998
df riv lambda fmi
1 28.06200 3.360105 0.7706478 0.7854151
2 30.54513 2.855070 0.7406014 0.7560670
The estimate column is just the averages of all m models. Full details about the computation on these columns are provided by Rubin (1987) on pages 76 and 77. The columns are explained as follows:
estimate: the average of the regression coefficients acrossmmodels.ubar: the average variance (i.e., averageSE^2) acrossmmodels.b: the sample variance of themregression coefficients.t: a final estimate of theSE^2 of each regression coefficient.=
ubar + (1 + 1/m) * b
dfcom: the degrees of freedom associated with the final regression coefficient estimates.An
alpha-level confidence interval:estimate +/- qt(alpha/2, df) * sqrt(t).
riv: the relative increase in variance due to randomness.=
t/ubar - 1
lambda: the proportion of total variance due to missingness.fmi: the fraction of missing information.
Where are the usual outputs (std.error, p.value,…)?
We can call summary() on the pooled model to obtain them. The usual coefficient interpretations and inferential rules also apply in this pooled OLS model.
summary(pooled_PMM_LR_model)
| term | estimate | std.error | statistic | df | p.value |
|---|---|---|---|---|---|
| <fct> | <dbl> | <dbl> | <dbl> | <dbl> | <dbl> |
| (Intercept) | 28.262276 | 4.76774255 | 5.927811 | 28.06200 | 2.203849e-06 |
| dep_delay | 0.833603 | 0.02664978 | 31.279914 | 30.54513 | 9.205948e-25 |
3. Wrapping Up#
Data imputation involves some wrangling effort and proper missingness visualizations.
We have to be careful when defining our class of data missingness since this will determine the type of data imputation we need to make (or maybe data deletion!).
In general, multiple imputation will work OK for MAR and MNAR data.
We only saw continuous imputation in this example. Nonetheless, the
mice()approach can be extended to other data types such as binary or categorical. In those cases, we have to switch to generalized linear models (GLMs), even with a Bayesian approach such as multiple imputation.